POEM: POpulation Epidemiological Model for anti-epidemic measures efficiency prognosis in the Russian Federation

Full Text

Введение

Пандемия COVID-19 показала, что социально-экономические факторы являются объективным ограничением при реализации необходимого комплекса противоэпидемических мероприятий. Разные страны выбрали различные подходы к предотвращению распространения новой коронавирусной инфекции, во всех случаях аргументируя обоснованность принимаемых решений. На этом фоне стала очевидной потребность в вычислительных эпидемиологических моделях, которые позволили бы максимально объективно оценивать потенциальный эффект отдельных противоэпидемических мероприятий и соотносить его с социально-экономическими потерями от эпидемии. Таким образом, пандемия COVID-19 послужила стимулом для развития методов компьютерного моделирования эпидемий.

Вычислительные модели для изучения распространения инфекционных болезней можно разделить на два основных типа: компартментные и агентные. Компартментные модели появились почти 100 лет назад и активно использовались благодаря скорости и лёгкости выполнения расчётов. В базовой компартментной модели (SIR — Susceptible, Infected, Recovered — восприимчивые, инфицированные, выздоровевшие) все индивидуумы одинаковые и могут находиться только в трех состояниях. Хотя описаны модификации SIR-модели для анализа дополнительных параметров, учёт индивидуальных комбинаций свойств субъектов, составляющих популяцию, практически не осуществляется. Агентные модели позволяют наделить каждого из виртуальных субъектов уникальными характеристиками любой сложности. Они намного более затратные в вычислительном отношении, но позволяют создавать цифровую среду, наиболее точно воспроизводящую условия развития эпидемического процесса [1].

Сложность разработки привела к распространению практики использования готовых агентных моделей с открытым кодом, который дорабатывается пользователем для решения спектра конкретных задач. Из рассмотренных основных вычислительных подходов к созданию искусственных популяций, агентом которых выступает человек, наибольшее распространение в моделировании респираторных инфекций получили платформы FRED [2], AceMod и Covasim [3].

Платформа с открытым кодом Covasim выгодно отличается тем, что содержит множество встроенных алгоритмов моделирования противоэпидемических мероприятий и предоставляет возможность модификации программного кода для реализации дополнительные функций. Она была использована для решения самых разных задач, например, определения оптимальной стратегии тестирования бессимптомных носителей [4], моделирования социркуляции разных геновариантов SARS-CoV-2 [5], эффекта отмены закрытия школ [6] и вероятности «второй волны» [7] в Великобритании, разработки стратегии борьбы с пандемией [8, 9] и вакцинации [10] в Австралии, стратегии вакцинации в США [11] и Италии [12]. При этом в большинстве работ использовалась модель, доработанная с учётом региональных особенностей и конкретных задач.

Цель работы — разработка эпидемиологической агентной модели ПОЭМА (ПОпуляционная Эпидемиологическая Модель Агентная) на базе платформы Covasim для моделирования эпидемий, изучения влияния различных факторов на распространение возбудителей и оценки эффективности противоэпидемических мероприятий в искусственной популяции. Применение созданного вычислительного инструмента было продемонстрировано в серии цифровых экспериментов в сопоставлении с наблюдаемыми эпидемиологическими закономерностями.

Материалы и методы

В качестве основы для разработки использовали открытый исходный код программы Covasim, выпущенный под допускающей свободное использование лицензией Creative Commons Attribution-ShareAlike 4.0 и доступный на сервере GitHub (github.com/institutefordiseasemodeling/covasim). ПОЭМА, как и Covasim, реализована на языках программирования Python и JavaScript.

Моделирование двух и более населённых пунктов с учётом их взаимодействия

Симуляция 2 и более населённых пунктов реализована с применением параллельных вычислений следующим образом: на этапе инициализации в каждом городе создаются дополнительные ячейки для агентов, которые могут прибыть в этот город. Затем каждый город моделируется в отдельном вычислительном потоке. Основная симуляция включает три этапа: добавление агентов, приехавших в город, выполнение основного шага симуляции (один условный день) и выбор агентов, которые покинут город на следующем шаге симуляции. Для каждого перемещённого агента длительность пребывания в другом городе выбирается исходя из распределения Пуассона со средним значением 14 дней (параметр может быть изменён пользователем). У агента, переместившегося на время из одного населённого пункта в другой, остаются только случайные взаимодействия, но их количество возрастает в среднем в 3 раза (коэффициент может быть изменён пользователем). В графический интерфейс добавлена возможность задавать один и более транспортных потоков (перемещение агентов между населёнными пунктами), пользователь указывает исходный пункт и пункт назначения, а также долю ежедневно перемещаемых агентов. Также в графическом интерфейсе реализована возможность просматривать результаты моделирования по отдельным локациям в разных вкладках или сравнить их на общем графике.

Моделирование проведения массовых мероприятий

Симуляция массовых мероприятий реализована следующим образом: пользователь подаёт на вход таблицу (через графический интерфейс или через вызов функций на языке Python), содержащую для каждого мероприятия день проведения, количество участников и количество таких собраний. Для реализации данного модуля был добавлен новый слой контактов. Этот слой является динамическим, контакты в нём обновляются каждый день для симуляции новых мероприятий. Один агент может участвовать только в одном мероприятии за день.

На первом шаге случайным образом определяется список агентов, которые будут участвовать в массовых мероприятиях. Далее участники разбиваются на группы по отдельным мероприятиям. Для каждой группы строятся случайным образом контакты так, чтобы в среднем у каждого агента было 9 связей, поскольку, по данным литературы, даже для больших массовых мероприятий число контактов с продолжительностью 15 мин и более, при которых возможна передача вируса, в среднем равно 9 [13]. Коэффициент вероятности передачи инфекции при контакте для массовых мероприятий принят равным таковому для рабочих контактов.

Функциональные расширения модели Covasim, реализованные в платформе ПОЭМА

Введены новые варианты распределений восприимчивости агентов к возбудителю и их заразности. Реализован вариант, при котором агенты имеют индивидуальные, но одинаковые для данного агента значения восприимчивости и заразности, с целью моделирования поведения агентов с высокими значениями обоих показателей.

Добавлен учёт задержки по времени между получением положительного результата тестирования и датой передачи информации в органы государственного контроля. Каждому агенту назначается задержка в получении результатов тестирования (случайное число из заданного распределения), которая в ходе симуляции прибавляется к дате проведения теста.

Для учёта социально-демографических особенностей моделируемых регионов РФ реализован дополнительный модуль настройки построения искусственной популяции. Модуль реализован на основе библиотеки с открытым исходным кодом synthpops (доступен по ссылке: https://github.com/InstituteforDiseaseModeling/synthpops). В интерфейс была добавлена возможность загрузки параметров искусственной популяции в формате таблицы Excel.

Добавлен набор параметров возбудителя, соответствующих варианту Omicron, на основе литературных данных. Совокупность факторов моделирования варианта Omicron вируса SARS-CoV-2 отбирали на основании поиска литературы в базах данных PubMed и Google Scholar по следующим ключевым словам: Omicron transmissibility, transmissibility of Omicron, symptomatic factor, critical factor of Omicron, severe factor of Omicron, death factor of Omicron and recovery of asymptomatic Omicron. Поиск проводили для статей, опубликованных с 2021 г., были отобраны 45 публикаций, в которых представлены необходимые для стохастической агентной модели параметры. Для расчёта среднего медианного значения этих параметров использовали только те работы, в которых размер выборки был не менее 100 человек.

Вычислительные эксперименты проводили в 2 этапа: сначала с использованием Web-интерфейса оценивали результат при различных сценариях без повторов, затем для оценки вариабельности результатов из-за стохастического характера модели наиболее информативные сценарии посредством скрипта на языке Python выполнялись 30 или 100 раз (в разных задачах).

Результаты

Модификации исходного кода Covasim

Создание ПОЭМА было осуществлено на базе открытой среды программирования Covasim с модификацией или добавлением кода в конкретные модули для внедрения новых функций, повышения информативности и локализации (табл. 1).

 

Таблица 1. Сопоставление Covasim и ПОЭМА

Covasim	ПОЭМА
Восприимчивость агента к возбудителю задана дискретно в зависимости от возрастной категории	Восприимчивость агента к возбудителю задаётся согласно выбранному варианту распределения
Заразность агента задаётся распределением, независимым от восприимчивости агента	Заразность агента может быть задана совместно с восприимчивостью данного агента
Моделирование распространения вариантов SARS-CoV-2 — Уханьский вариант, Alpha, Beta, Gamma, Delta	Введена возможность моделирования инфекции, вызванной вариантом SARS-CoV-2 Omicron; есть возможность создания пользовательского варианта вируса
Моделирование эпидемического распространения происходит в одной синтетической популяции (условном городе), которая создаётся на основании усреднённых европейских демографических и статистических данных	Моделирование эпидемического распространения происходит параллельно для множества синтетических популяций (условных городов) с различными задаваемыми параметрами. Модельные города задаются независимыми друг от друга или связанными коэффициентом взаимодействия. Имеется возможность построения модельных городов на основании реальных демографических и статистических данных
Возможность моделирования противоэпидемических мер — карантин, масочный режим, вакцинация	Добавлена возможность моделирования как разовых (единичных), так и регулярных массовых мероприятий
Противоэпидемические мероприятия вводятся одновременно и с одинаковой интенсивностью во всех учреждениях одного типа условного города	Есть возможность выборочно «закрывать» отдельные школы и предприятия при достижении определённого процента диагностированных случаев (эпидемический порог)
Результаты тестирования агентов отражаются на графике заболеваемости в день тестирования	Результаты тестирования отображаются на графике заболеваемости с задержкой, рассчитанной на основании реальных данных Роспотребнадзора (18 млн записей)
Для настройки требуются базовые навыки программирования	Настройка параметров и расширенные возможности для визуализации в Web-версии

 

1. Назначение агентам распределения восприимчивости и заразности

Ключевыми параметрами инфекционного процесса являются восприимчивость субъектов к инфекции (врождённый и приобретённый иммунитет) и контагиозность (заразительность) — возможность передачи возбудителя от субъекта к субъекту. При этом контагиозность считается характеристикой патогена, поскольку на популяционном уровне индивидуальные характеристики субъектов усредняются. В агентной модели имеется возможность задавать индивидуальную способность агента распространять вирус (например, за счёт более высокого уровня репликации вируса, особенностей поведения, выраженности симптомов респираторной инфекции или уменьшения заражающей дозы). Для описания этой характеристики агента (субъекта) далее будет использоваться термин «заразность».

Исходный код Covasim предполагает задание восприимчивости агентов к вирусу, жёстко привязанное к возрасту агента (табл. 2) [14]. При этом авторы Covasim отмечают, что принятые ими характеристики восприимчивости противоречат результатам другого исследования, где восприимчивость к инфекции не менялась с возрастом [15]. В то же время очевидно, что восприимчивость агентов должна соответствовать математическим распределениям, обычно наблюдаемым в биологии, и в других исследованиях изучалось, например, распространение инфекции в популяции при использовании равномерного, гауссова и бимодального гауссова распределений [16].

 

Таблица 2. Коэффициенты восприимчивости возрастных групп населения к вирусу SARS-CoV-2, принятые в исходной версии Covasim [14]

Показатель	Возраст, лет
	0–9	10–19	20–29	30–39	40–49	50–59	60–69	70–79	80–89	90+
Восприимчивость*, %	0,34	0,67	1,00	1,00	1,00	1,00	1,00	1,24	1,47	1,47

Примечание. *Коэффициент вероятности заражения при контакте между агентами, используемый в составе формулы, определяющей вероятность передачи вируса при каждом контакте.

 

Поскольку точные характеристики распределения восприимчивости людей к SARS-CoV-2 и другим респираторным вирусам неизвестны, в модель ПОЭМА была включена возможность применения следующих нормированных распределений:

• распределение восприимчивости с учётом возраста агентов, предложенное в базовой модели Covasim (табл. 2);
• нормальное (без зависимости от возраста);
• логнормальное (без зависимости от возраста);
• логнормальное резкое, с тонким хвостом (без зависимости от возраста).

Для того чтобы обеспечить возможность сравнения влияния распределения восприимчивости на параметры распространения инфекции, сумма условной восприимчивости агентов в популяции (площадь под кривой распределения восприимчивости) в модели ПОЭМА является константой.

В исходном коде Covasim у агента задаётся характеристика восприимчивости (табл. 2), а заразность определяется вероятностью передачи возбудителя. Однако при распространении COVID-19 описана выраженная гетерогенность по числу заражений от одного больного, когда 80% вторичных заражений были обеспечены 15% больных [17]. Также известно, что вариабельность количества вируса SARS-CoV-2 при исследовании методом полимеразной цепной реакции у разных больных (соответственно, и возможность передачи вируса) составлял несколько порядков [18]. В модели ПОЭМА была введена возможность установить прямую зависимость между восприимчивостью субъекта к вирусу и его заразностью либо задавать эти параметры как несвязанные, поскольку в литературе имеются данные в пользу обоих вариантов. Например, способность заражаться и поддерживать высокий уровень репликации теоретически может быть связана с уровнем экспрессии рецептора к вирусу [19]. С другой стороны, показано, что некоторые люди производят значительно больше микрокапель, чем другие, и могут быть более заразны только за счёт этого [20], т. е. восприимчивость и заразность могут быть не связаны между собой на индивидуальном уровне.

2. Введение временно́й задержки при отражении результатов тестирования

Одним из недостатков базового кода Covasim является мгновенное получение результатов тестирования, проводимых на искусственной популяции агентов. При этом фактическая регистрация данных о тестировании в общей статистике в условиях повышенной нагрузки на систему здравоохранения может происходить со значительной задержкой. Интеграция в модель ПОЭМА реалистичной задержки, максимально приближенной к условиям регистрации заболеваемости в России, выполнена на основании анализа записей более чем 18 млн случаев заболевания COVID-19, для которых сравнивали дату забора положительной пробы и дату поступления информации в Роспотребнадзор. Полученное распределение разницы этих дат для каждого образца было использовано для определения вероятности получения данных с задержкой после проведения тестирования (табл. 3).

 

Таблица 3. Распределение задержки поступления информации о положительных результатах тестирования в Роспотребнадзор, дни после забора анализа

Показатель	Задержка, дни
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Доля, %	< 1	14	22	12	10	9	7	6	5	4	3	2	2	2	2

 

3. Внедрение блока формирования двух и более населённых пунктов с их взаимодействием или без взаимодействия

Пандемия COVID-19 продемонстрировала, что введение изоляции определённой территории или населённого пункта не может гарантировать предотвращение распространения возбудителя. Для формирования политики здравоохранения на уровне страны моделирование эпидемии в отдельно взятом регионе без учёта взаимосвязи с другими регионами имеет ограниченную ценность. В исходном коде Covasim реализована опция моделирования притока фиксированного числа заражённых в моделируемую популяцию (каждый день заданное число агентов заболевают без источника заражения), при этом отток инфицированных агентов не предусмотрен. Такой подход не позволяет учитывать динамику развития эпидемии в связанных регионах. Для преодоления этого ограничения была разработана возможность параллельного моделирования нескольких популяций (городов) с независимыми параметрами противоэпидемических мероприятий и возможностью регулировать движение агентов между ними. При отсутствии взаимодействия между городами каждый из них может рассматриваться как независимый эпидемиологический эксперимент, что позволяет сравнивать эффект от особенностей популяции или характера противоэпидемических мероприятий. Коэффициент взаимодействия городов задаётся эмпирически как процент населения, «перетекающий» между городами каждый день, отражая условные транспортные потоки.

4. Построение модельной искусственной популяции на основании реальных демографических и социологических данных

Моделирование эпидемического процесса в условиях, приближенных к реальным социумам, реализовано в модели ПОЭМА через возможность загрузки демографических и социологических данных конкретного населённого пункта или региона. Данные предоставляются пользователем в виде электронной таблицы, сформированной согласно шаблону, и включают в себя численность населения и его распределение по возрасту, распределение размеров домохозяйств, размеры учебных заведений и количество работающих в них преподавателей и прочих работников, распределение размеров рабочих коллективов и долю занятого населения.

В качестве примера реализации загрузки реальных данных в модели ПОЭМА созданы профили субъектов РФ: Благовещенск и Амурская область, Нижний Новгород и Нижегородская область, Воронеж и Воронежская область.

5. Моделирование распространения варианта Оmicron

В конце ноября 2021 г. Всемирная организация здравоохранения определила новый генетический вариант SARS-CoV-2 как вызывающий озабоченность (B.1.1.529) с присвоением названия Оmicron [21]. На момент появления у этого варианта SARS-CoV-2 было в несколько раз больше мутаций в шиповидном белке, чем у любого другого варианта [22]. Благодаря этим мутациям вирус варианта Оmicron более эффективно связывается с рецепторами ACE2 клетки-хозяина по сравнению с предшествующими вариантами. На Оmicron не действуют большинство нейтрализующих антител, вырабатываемых вакцинированными или переболевшими другими вариантами SARS-CoV-2, однако он ассоциируется с более лёгкими симптомами и большей долей бессимптомных носителей по сравнению с другими вариантами [23].

Степень опасности варианта коронавируса зависит от таких факторов, как заразность, уклонение от иммунитета и тяжесть клинического течения инфекции [24]. Базовый репродуктивный показатель (R₀) варианта Оmicron составляет 8,2 [25], что соответствует намного более эффективному распространению по сравнению с более ранними вариантами вируса. В исходной среде Covasim задание трансмиссивности вариантов вируса реализовано на основании коэффициентов относительно исходного Уханьского варианта. В модели ПОЭМА вероятность передачи инфекции от агента к агенту была задана равной 3,34 (относительно Уханьского варианта), рассчитанной как среднее, полученное на основании анализа нескольких публикаций. Вероятность симптоматического течения инфекции при заражении вариантом Оmicron была установлена в 0,1 на основании многоцентрового ретроспективного обсервационного исследования, проведённого в Шанхае [26]. Риск госпитализации при инфекции вариантом Оmicron был на 56% ниже по сравнению с вариантом Delta [27], а риск тяжёлого течения в 2–3 раза ниже [28]. На основании систематического обзора и метаанализа тяжести и клинических исходов у людей, переболевших вариантом Оmicron, был использован коэффициент вероятности критической тяжести заболевания 0,46 по сравнению с вариантом Delta, а коэффициент вероятности летального исхода 0,39. По данным литературы, инкубационный период (в терминологии платформы Covasim, на самом деле латентный период, время от заражения до начала выделения вируса) для варианта Оmicron составляет около 2–3 дней, а средняя длительность бессимптомного периода — 2,2 дня [29].

Медианная продолжительность обнаружения вируса составляла 9 дней (от 7 дней у бессимптомных до 10 дней при тяжёлом течении заболевания) [30]. Острые симптомы у инфицированных вариантом Оmicron наблюдались в течение менее длительного периода — в среднем 6,9 дня, чем у пациентов, инфицированных Delta, — в среднем 8,9 дня [24]. Продолжительность пребывания в отделениях интенсивной терапии при заражении вариантом Оmicron была на 5 дней меньше, чем при заражении вариантом Delta, среднее медианное значение составило 5,3 дня [31]. Общий уровень летальности был выше для пациентов с вариантом Delta и составил 0,5% по сравнению с пациентами с вариантом Оmicron (0,1%). Средний интервал от постановки диагноза до смерти при заражении вариантом Delta составлял 13 дней по сравнению с 10 днями при варианте Оmicron [31].

Вычислительные эксперименты

1. Моделирование массовых мероприятий

Массовые мероприятия оказывают значительное влияние на динамику развития эпидемий [32–34] и являются одной из приоритетных мишеней противоэпидемических мероприятий.

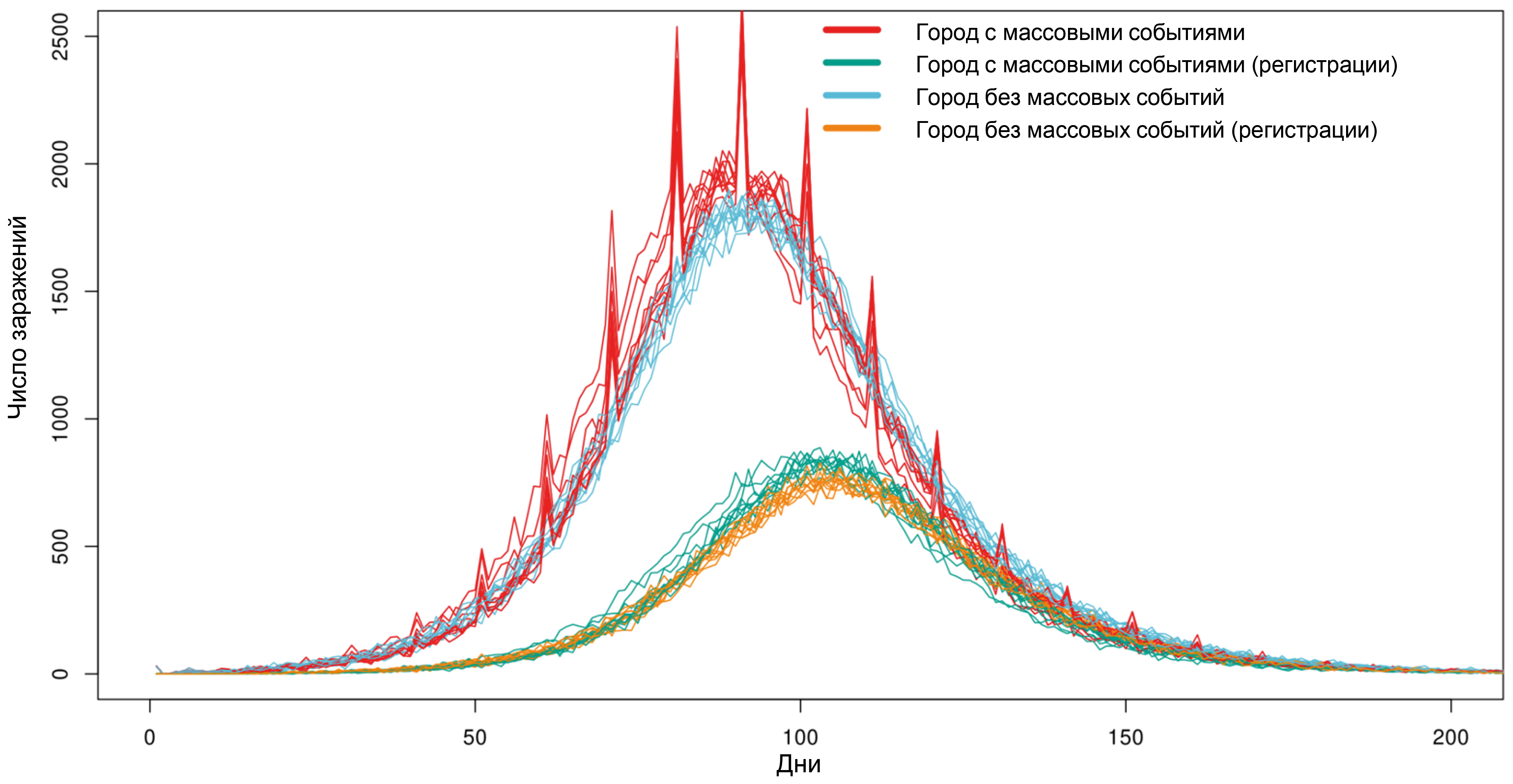
Заданы 2 города с населением 100 тыс. жителей с введёнными противоэпидемическими мерами в виде социального дистанцирования (снижение частоты случайных контактов на 50%, контактов в школе и на работе — на 90%). В начальный день в обоих городах 30 человек инфицированы SARS-CoV-2, вариант Delta. Вероятности тестирования бессимптомных и проявляющих симптомы агентов составляли 1 и 10% соответственно. Каждые 10 дней в одном из городов проводятся массовые мероприятия с общим числом участников, равным 20 тыс. Результаты 10 симуляций каждого города представлены на рис. 1. Проведение массовых событий приводит к резкому повышению количества инфицированных в модели. Однако даже значительное количество одномоментно заражённых (500–1000 на фоне 1000–2000 обычно инфицируемых в день) невозможно выявить по результатам ежедневного тестирования из-за сглаживания заболеваемости за счёт разной длительности латентного периода и неравномерной задержки поступления информации о положительных результатах, которая нивелирует резкие подъёмы инфицирования.

 

Рис. 1. Влияние проведения массовых мероприятий на число инфицированных SARS-CoV-2 в городе размером 100 тыс. агентов.

 

2. Моделирование противоэпидемических мероприятий

Наиболее тяжёлое клиническое течение COVID-19 наблюдалось у лиц старшего возраста. Именно на защиту возрастной группы риска были направлены наиболее интенсивные противоэпидемические мероприятия. При этом одной из распространённых мер для снижения заболеваемости было закрытие школ для снижения распространения вируса в обществе и, как следствие, риска внутрисемейного заражения пожилых. Описаны отдельные примеры влияния закрытия школ на снижение заболеваемости пожилых [35], однако в целом эпидемиологические данные не подтверждают эффективность таких мер с достаточной степенью уверенности, а описанные ранее результаты математического моделирования были противоречивыми [36, 37].

На модели ПОЭМА были проверены следующие гипотетические сценарии. Максимально эффективные (100% разобщение всех контактов) меры применялись только к молодым (< 20 лет) или только к пожилым (> 60 лет) на 30–90-й или 60–120-й дни после начала эпидемии (на момент введения мер инфицировано приблизительно 1 или 20% населения соответственно), при этом исходили из того, что административный ресурс позволяет ввести ограничения только на 60 дней.

При раннем введении мер, на фоне низкой распространённости COVID-19, наблюдался выраженный эффект на число инфицированных, однако из-за отмены ограничений на 90-й день, к 140-му дню количество инфицированных во всех группах практически не различалось (рис. 2). При этом изоляция и молодых, и, особенно, пожилых привела к снижению числа смертей на 17 и 35% соответственно, однако доверительные интервалы этих результатов частично перекрывались.

 

Рис. 2. Влияние введения противоэпидемических мер для разных возрастных групп на заболеваемость и смертность.

Синим на графике отмечены результаты при изоляции молодых индивидов, красным — при изоляции пожилых. Зелёным — моделирование эпидемии в городе без введения мер. Красным и зелёным показано ежедневное число инфицированных и регистрируемые на основании проведения тестирования случаи в городе с массовыми мероприятиями, голубым и жёлтым — число инфицированных и регистрируемые на основании проведения тестирования случаи в городе без массовых мероприятий.

 

При позднем введении мер изоляция молодых привела к снижению числа заболевших на 25%, однако снижение числа летальных исходов было менее выраженным — 16%. Поздняя изоляция пожилых привела к меньшему снижению общей заболеваемости, но к значительному снижению смертности (66%). Таким образом, изоляция молодых может оказать эффект на заболеваемость пожилых, но менее заметный, чем непосредственная изоляция пожилых.

Полученные результаты моделирования согласуются с представлениями о том, что позднее разобщение организованных детских и подростковых коллективов, осуществляемое на фоне роста заболеваемости COVID-19, сопровождается интенсификацией передачи инфекции в домашних очагах за счёт более длительного и тесного бытового контакта (учащиеся, переведённые на заочную форму обучения, инфицируют лиц пенсионного возраста, которые временно привлекаются к надзору за несовершеннолетними).

3. Моделирование пассажиропотоков

Во время пандемии COVID-19 введение ограничения на передвижение между городами и странами было практически повсеместным и ставило целью предотвратить занос вируса из регионов с неблагополучной эпидемической обстановкой в области. Для моделирования эффективности блокирования транспортных потоков была выполнена симуляция распространения эпидемии в двух городах. В обоих городах противоэпидемические меры вводили на 50-й день симуляции (мягкие меры в первом городе, жёсткие — во втором). На 90-й день симуляции в обоих городах проводились только мягкие противоэпидемические меры, которые продолжались до окончания моделирования. Мягкие противоэпидемические меры включали только масочный режим на работе и в общественных местах с условной эффективностью 25%, жёсткие меры — масочный режим на работе и в общественных местах с условной эффективностью 75% и закрытие школ. Распространение эпидемии моделировалось при условии минимальных транспортных потоков (0,01% населения ежедневно перемещается между городами), средних (0,1% населения ежедневно, примерно соответствует транспортным потокам между Москвой и Санкт-Петербургом) и интенсивных (1% населения ежедневно).

В городе с мягкими мерами число заболевших к 200-му дню составило 60 тыс. (против 72 тыс. при отсутствии мер), умерших — 210 против 275 (рис. 3). При минимальных транспортных потоках число заболевших в городе с жёсткими мерами к 200-му дню составило 50 тыс., умерших — 130 человек. При средних транспортных потоках число заболевших в городе с жёсткими мерами практически не изменилось, число умерших выросло до 150 человек. При интенсивных транспортных потоках эффект от жёстких противоэпидемических мер во втором городе был практически нивелирован.

 

Рис. 3. Влияние транспортных потоков между городами при различном уровне введения противоэпидемических мер на заболеваемость и смертность.

Синим на графике показаны результаты симуляции для города с наибольшей эффективностью мер, красным — для города с мягкими мерами. Зелёным — моделирование эпидемии в городе без введения мер и с отсутствием транспортного сообщения. Пунктирные линии показывают даты введения и отмены мер и завершения симуляции.

 

4. Моделирование введения мер при достижении порогового значения случаев

Классическим инструментом в эпидемиологии является введение противоэпидемических мероприятий при достижении заданного уровня (эпидемический порог). Данная методика хорошо отработана для гриппа¹. Поскольку для COVID-19 значения эпидпорога не разработаны, в моделировании были проверены три достаточно строгих значения: 20, 70 и 150 случаев на 10 тыс. населения. При этом было принято, что административный ресурс ограничен, строгие меры (масочный режим с эффективностью 70% в общественных местах и на работе, закрытие школ) вводятся только на 30 дней, затем ещё на 30 — более мягкие (масочный режим с эффективностью 30% в общественных местах, на работе и в школах), Противоэпидемические меры оказали немедленный эффект на эффективность передачи возбудителя в модельной популяции (снижение эффективного репродуктивного числа ниже 1). Суммарное количество инфицированных составляло 30–35 тыс. во всех сценариях, но количество умерших в случае самого позднего введения мер (при достижении суммарного числа диагностированных случаев 150 на 10 тыс. населения) достигло 145, а во всех остальных сценариях значения находилось в диапазоне 91–111 человек (рис. 4). Таким образом, модель ПОЭМА позволяет симулировать развитие эпидемии в условиях использования принятых в России стандартов реагирования на распространение заболеваемости, а учёт задержки регистрации, основанный на реальных данных, позволяет планировать борьбу с распространением инфекции с учётом этого фактора.

 

Рис. 4. Влияние введения противоэпидемических мер при достижении порога зарегистрированных случаев на заболеваемость и смертность.

Синим на графике показаны результаты симуляции при введении мер при достижении порога в 20 диагностированных случаев, красным — при достижении порога в 70, зелёным — в 150 диагностированных, фиолетовым — моделирование эпидемии в городе без введения мер.

 

5. Моделирование циркуляции двух вариантов вируса

Для примера была выбрана Воронежская область, для которой было доступно достаточно большое количество полногеномных сиквенсов вируса SARS-CoV-2 на платформе VGARus в декабре 2021 г. – январе 2022 г., что позволяет сравнить расчётное соотношение вариантов вируса в симуляции и фактически наблюдаемое. В модель были загружены демографические данные и на их основе был создан «цифровой двойник» Воронежской области, в котором 01.04.2021 появились 30 агентов, инфицированных вариантом Delta, а 15.12.2021 — 30 агентов, инфицированных вариантом Omicron. Данная симуляция была повторена 100 раз, результаты представлены на рис. 5. Коэффициент корреляции Пирсона доли варианта Omicron среди циркулирующего в популяции SARS-CoV-2 между средним результатом из 100 симуляций и реальными данными составил 0,9985.

 

Рис. 5. Симуляция смены доминирующего варианта SARS-CoV-2 в Воронежской области зимой 2021–2022 гг.

а — график ежедневного числа инфицированных с разбивкой по вариантам SARS-CoV-2. Вариант Delta обозначен зелёным цветом, вариант Omicron — красным. Графики ежедневного числа инфицированных в 100 симуляциях отображены бледными цветами, усреднённые значения — яркими.

б — доля варианта Omicron среди циркулирующего в Воронежской области SARS-CoV-2. Вычисленные по результатам 100 симуляций значения отображены бледно-синим цветом, усреднённое значение — тёмно-синим, реальные данные по результатам анализа полногеномных сиквенсов — красным.

 

Обсуждение

Вычислительная эпидемиология представляет собой новую область знаний, объединяющую принципы классической эпидемиологии, статистики, математики и информатики для анализа больших массивов данных, моделирования распространения заболеваний в человеческой популяции и обоснования политики общественного здравоохранения.

Успешным примером реализации такого подхода является модель Барояна–Рвачева для предсказания эпидемии гриппа в СССР [38]. В модели использовались подробные данные междугородних миграционных потоков, что позволило прогнозировать моменты старта эпидемического процесса и наступление его пика в столицах союзных республик с высокой точностью.

Быстрое развитие вычислительных технологий в конце XX в. – начале XXI в. позволило перейти к широкомасштабному агентному моделированию с явными взаимодействиями между индивидуумами для симуляции распространения инфекционных болезней. Разработка таких подходов позволяет учитывать целый ряд принципиальных особенностей: разнообразие агентов (например, возраст, пол, социальный статус и т. д.), неоднородность социальных контактов, миграционные потоки, введение мероприятий по контролю распространения заболевания для отдельных групп населения и т. д. Пандемия COVID-19 в полном объёме продемонстрировала необходимость использования предсказательной силы стохастических дискретных моделей для проведения вычислительных эпидемиологических экспериментов по подбору оптимального набора мер реагирования.

Платформа агентного моделирования Covasim, совмещённая с модулем создания синтетической популяции SynthPops, на сегодняшний день является одной из наиболее совершенных в эпидемиологии. За последние 3 года на базе Covasim выполнен большой объём исследований по разработке мероприятий для предотвращения распространения эпидемий, например:

• изучение стратегий тестирования и влияния характеристик тестов [4, 9, 39];
• изучение эффективности изоляции и карантина [6, 39];
• моделирование достижения коллективного иммунитета [10];
• анализ стратегий вакцинации [6, 11, 12];
• оценка рисков последствий отмены управленческих решений [8, 40].

В ряде случаев решение поставленных задач достигалось за счёт расширения, калибровки или модификации модели Covasim. Наиболее масштабные дополнения были предложены в новой модели ProMES на основе Covasim [41].

В данной работе представлена модель ПОЭМА, в которой преодолены ограничения, связанные с использованием платформы Covasim для населения разных регионов Российской Федерации и добавлен ряд новых функций, позволяющих проводить вычислительные эксперименты с большей детализацией и достоверностью, чем предусмотрено исходным кодом.

Реализованы профили восприимчивости агентов к SARS-CoV-2, которые отражают накопленные современные данные, отличные от результатов ранних исследований по COVID-19. Внедрена структура популяции на основе реальных демографических данных и корректная задержка регистрации на основе анализа 18 млн случаев COVID-19. Добавлена возможность оценки роли массовых мероприятий и транспортных потоков, на основе метаанализа опубликованных данных добавлена возможность симуляции заболеваемости вариантом Omicron. Web-интерфейс для запуска симуляции и визуализации результатов делает возможным работу с платформой ПОЭМА для пользователей без навыков программирования. Для научных исследований существует возможность множественных повторов симуляции с оценкой статистической значимости и выдачей результатов не только в графическом формате, но и в виде исходных значений всех параметров.

Выполненные для демонстрации возможностей модели цифровые эпидемиологические эксперименты показывают соответствие модели реально наблюдаемому развитию эпидемий и эффекту от противоэпидемических мероприятий. При этом на модели возможно отработать не только стандартные сценарии, но и экстремальные, такие как появление высоко контагиозных патогенов. Поскольку в течение пандемии COVID-19 ключевым ограничением стало принятие ограничений обществом, с использованием платформы ПОЭМА возможно подобрать максимально эффективные меры с учётом ограниченного административного ресурса. Модель Covasim была разработана с упором на производительность, простоту использования и гибкость: реалистичные сценарии можно запустить на стандартном ноутбуке менее чем за минуту [3]. В системе ПОЭМА моделирование эпидемии в популяции размером 100 тыс. человек в течение 180 дней и создание всех графиков выполняется за 30 с на системе с одним вычислительным ядром. Моделирование популяции в 1 млн человек в течение 180 дней занимает 6 мин.

Ограничением платформы ПОЭМА является отсутствие функций предсказания развития эпидемии. Существуют исследования, где такая возможность реализована за счёт динамической подстройки эффективности передачи вируса с учётом текущих данных о заболеваемости. Этот подход может быть достаточно эффективным для предсказания заболеваемости на короткий срок (порядка 2 нед), однако в данной работе приоритетной целью было максимально подробное воспроизведение популяции и распространения эпидемии для разработки стратегий противоэпидемических мероприятий. Динамическая подстройка модели является лёгким способом компенсировать несовершенство модели, однако может снизить её ценность как инструмента планирования.

Заключение

ПОЭМА — первая в России платформа для агентного моделирования эпидемий, в перспективе доступная широкому кругу профессиональных эпидемиологов. Гибкость модели позволяет практически неограниченно масштабировать платформу за счёт добавления регионов и транспортных потоков на основе демографических и статистических данных, задания новых вариантов коронавируса и других патогенов. Модель реализована полностью в российском контуре на сервере НИИ системной биологии и медицины Роспотребнадзора и может быть использована для проведения цифровых эпидемиологических экспериментов с целью прогноза эффективности противоэпидемических мероприятий в Российской Федерации.

 

¹ Государственное санитарно-эпидемиологическое нормирование Российской Федерации. 3.1.2. Инфекции дыхательных путей. Методика расчёта эпидемических порогов по гриппу и острым респираторным вирусным инфекциям по субъектам Российской Федерации. Методические рекомендации. МР 3.1.2.0118-17. М.; 2017.

About the authors

Anna Yu. Popova

Federal Service for Supervision of Consumer Rights Protection and Human Welfare

Email: samoilov_ae@sysbiomed.ru
ORCID iD: 0000-0003-2567-9032

D. Sci. (Med.), Professor, Head

Russian Federation, Moscow

Asiya F. Ayupova

Research Institute for Systems Biology and Medicine

Email: asiya.bun@gmail.com
ORCID iD: 0000-0002-7038-3911

researcher, Laboratory of molecular epidemiology of emerging infections

Russian Federation, Moscow

Vadim M. Govorun

Research Institute for Systems Biology and Medicine

Email: govorun@sysbiomed.ru
ORCID iD: 0000-0003-0837-8764

Dr Sci. (Biol.), Professor, Academician of the Russian Academy of Sciences, Director

Russian Federation, Moscow

Alina A. Gorbacheva

Research Institute for Systems Biology and Medicine

Email: mantodea13@gmail.com
ORCID iD: 0009-0009-7750-370X

researcher, Laboratory of molecular epidemiology of emerging infections

Russian Federation, Moscow

Elena N. Ilina

Research Institute for Systems Biology and Medicine

Email: ilinaen@sysbiomed.ru
ORCID iD: 0000-0003-0130-5079

Dr Sci. (Biol.), Corresponding Member of the Russian Academy of Sciences, main researcher, Head, Laboratory of mathematical biology and bioinformatics

Russian Federation, Moscow

Viacheslav N. Kachalov

Research Institute for Systems Biology and Medicine; Moscow Institute of Physics and Technology, National Research University

Email: kachalov_vn@sysbiomed.ru
ORCID iD: 0000-0002-0310-3764

senior researcher, Laboratory of mathematical biology and bioinformatics, Research Institute of Systems Biology and Medicine; Associate Professor, Moscow Institute of Physics and Technology (National Research University)

Russian Federation, Moscow; Dolgoprudny

Ivan E. Kozlov

Research Institute for Systems Biology and Medicine

Email: ivan.kozzloff98@gmail.com
ORCID iD: 0009-0007-2437-5527

assistant researcher, Laboratory of mathematical biology and bioinformatics

Russian Federation, Moscow

Konstantin A. Klochkov

Research Institute for Systems Biology and Medicine; Moscow Institute of Physics and Technology, National Research University

Email: konstantin.a.klochkov@gmail.com
ORCID iD: 0009-0008-2839-6189

junior researcher, Laboratory of mathematical biology and bioinformatics, Research Institute of Systems Biology and Medicine; student, Moscow Institute of Physics and Technology (National Research University)

Russian Federation, Moscow; Dolgoprudny

Vladimir V. Kutyrev

Russian Research Anti-Plague Institute “Microbe”

Email: rusrapi@microbe.ru
ORCID iD: 0000-0003-3788-3452

Dr Sci. (Med.), Professor, Academician of the Russian Academy of Sciences, Director

Russian Federation, Saratov

Alexander N. Lukashev

Research Institute for Systems Biology and Medicine; Sechenov First Moscow State Medical University

Email: alexander_lukashev@hotmail.com
ORCID iD: 0000-0001-7365-0352

Dr Sci. (Biol.), Corresponding Member of the Russian Academy of Sciences, main researcher, principal researcher, Research Institute of Systems Biology and Medicine; Director, Martsinovsky Institute of Medical Parasitology, Tropical and Vector Borne Diseases, Sechenov First Moscow State Medical University

Russian Federation, Moscow; Moscow

Alexander I. Manolov

Research Institute for Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0000-0003-3912-429X

Cand. Sci. (Biol.), researcher, Scientific

Russian Federation, Moscow

Irina I. Maslova

Research Institute for Systems Biology and Medicine

Email: maslova1ira@gmail.com
ORCID iD: 0009-0000-0849-9123

junior researcher, Laboratory of mathematical biology and bioinformatics

Russian Federation, Moscow

Andrei E. Samoilov

Research Institute for Systems Biology and Medicine

Author for correspondence.
Email: samoilov_ae@sysbiomed.ru
ORCID iD: 0000-0001-8284-3164

researcher, Laboratory of mathematical biology and bioinformatics

Russian Federation, Moscow

Valentin A. Safronov

Russian Research Anti-Plague Institute “Microbe”

Email: safronov64@gmail.com
ORCID iD: 0000-0001-9563-2833

leading redearcher

Russian Federation, Saratov

Vera I. Tsurkis

Research Institute for Systems Biology and Medicine

Email: veratsurkis21@gmail.com
ORCID iD: 0009-0001-5140-0990

junior researcher, Laboratory of mathematical biology and bioinformatics

Russian Federation, Moscow

References

Supplementary files