Limitations in creating artificial populations in agent-based epidemic modeling: a systematic review

Full Text

Introduction

Since the early 2000s, humanity has faced a number of viral epidemics, including Severe Acute Respiratory Syndrome (SARS, 2002-2003), Influenza A(H1N1)-California (swine flu) (2009), Middle East Respiratory Syndrome (MERS, 2012), Ebola outbreaks (2014-2016), Zika fever (2015-2016) and finally the COVID-19 pandemic caused by the novel SARS-CoV-2 coronavirus (2019-present). The COVID-19 pandemic has sparked the interest of epidemiology and public health professionals in using computational tools to predict epidemics and select optimal anti-epidemic measures. These tools include machine learning methods and computational epidemiologic models.

Computer simulations in epidemiology are designed to reproduce the dynamics of infectious disease spread, taking into account population demographics [1–3], contact network structure [4] and information on intervention strategies [5, 6]. These models provide a virtual laboratory to study hypothetical scenarios, evaluate the effectiveness of different interventions, and anticipate outbreak trajectories.

Numerical solution of ordinary differential equations and agent-based modeling (ABM) are the two most common modeling approaches in epidemiology [7, 8]. The first approach includes various compartmental models, such as the susceptible-infected-uninfected model [9] and its modifications; the second approach includes agent-based models, which take into account the heterogeneity of a population by modeling the actions and interactions of individual agents (people) within it [3, 4, 10].

Agent-based models consider each person as an autonomous agent with characteristics that determine his/her behavior and social interactions. The semantic blocks into which any synthetic population can be divided are presented in Fig. 1.

 

Fig. 1. The artificial population consists of agents with different demographic characteristics (block A). These agents are assigned specific tasks to perform at specific locations and times. This determines a network that connects agents to locations throughout the day, creating a person-location network (Block В). The person-to-person contact network (Block Б ) is developed based on the interactions obtained from the person-to-location graph.

 

The agent-based approach is applicable for studying epidemic control measures [11–13], assessing the effectiveness of interventions on different populations [14], and conducting sensitivity analysis of modeling results to changes in parameter values [15]. The main goals of public health applications of ABM are to analyze and predict the public health consequences of proposed interventions, taking into account aspects of complex social structure. ABM-based models help to understand the underlying mechanisms that determine the dynamics and outcomes of epidemics. ABMs can be used for virtual experiments exploring different intervention strategies and other interventions to reduce morbidity in the population [16]. All this makes ABMs an important research and training tool for public health professionals.

The main difficulty in using ABM as a tool for social, political, and economic research lies in the proper matching of the purpose of modeling and the level of detail of the model [17]. The disadvantage of ABM can be excessive detail, which complicates the overall modeling task and leads to the creation of overly complex models with redundant parameters that do not contribute significantly to the modeling results [18].

Finding a balance in the choice of considered parameters and complexity when creating an artificial population (AP) for ABM is an open question facing researchers. This systematic review aims to identify the most common approaches to creating AP in agent-based modeling and to specify their limitations.

Materials and methods

This systematic review is based on the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) guidelines. A systematic literature search was conducted using the PubMed database. The search was performed using the keywords: "agent-based" AND "epidemiology". Full-text articles published between 2020 and 2024 were considered. The initial assessment selected studies that used agent-based modeling, studied respiratory viral infections, and had a sufficiently detailed description of the model.

 

Fig. 2. Publication selection scheme for the systematic review.

 

Papers studying the behavior of the virus in a single organism, as well as studies on modeling animal infections, were excluded from the study.

According to the search methodology, 144 studies published in international journals in English were selected and used for further analysis. No Russian-language publications meeting the selection criteria were found. The selected publications were systematized according to the ways of setting the AP by the criteria "location" (space consideration) and "agent properties". The agent's properties included such characteristics as gender, age, field of activity, ethnicity, income, and the like — i.e., characteristics determined on the basis of demographic and statistical data. We considered that the model accounted for locations if the probability of transmission depended on the agent's spatial location. This property of the model can be realized both by tracking the coordinates of each agent in the modeled space and by modeling individual spatial entities (e.g., store, school) that may house agents.

Results

In 2020-2024, the greatest interest of researchers was focused on modeling the spread of SARS-CoV-2 virus, the causative agent of COVID-19, in the population: 129 (89%) papers out of 144 selected modeled the spread of this virus, 10 (11%) papers modeled the spread of influenza virus. In several studies, researchers presented their models as suitable for studying several respiratory diseases (Table 1).

 

Table 1. Distribution of the articles according to the pathogen

Pathogen	Publication amount
	n	%
SARS-CoV-2	129	89
Influenza	10	6,9
Measles	1	0,7
MERS-CoV	1	0,7
Unspecified respiratory diseases	4	2,7

 

To systematize the types of APs used in the models, we analyzed the presence of agent properties and the consideration of their location. Fig. 3 shows the distribution of publications considered in the review according to the type of APs described in them.

 

Fig. 3. Distribution of publications by artificial population type. *Аt the same time, agents can be endowed with an individual level of protection against the pathogen (immunity) and the level of viral load. **Тhis group also includes papers that consider the spatial location of buildings and/or agents.

 

We can distinguish 4 variants of AP construction, based on combinations of presence and absence of consideration of agents' properties and consideration of locations.

Approaches to AP creation without consideration of location and agent properties (12 articles)

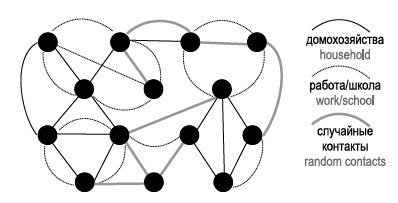
An artificial population without taking into account spatial localization and demographic properties of agents represents a graph — a network of contacting agents (Fig. 4). The stochasticity of such models is created by generating individual sets of connections at each node (agent) based on given probability distributions of the number of contacts.

 

Fig. 4. A network of contacts without considering the properties of agents and spatial characteristics is illustrated. Each node represents an agent, and the edges between nodes indicate a contact on one of the layers.

 

At the same time, contacts or social ties can be the same or differ in the strength and frequency of interaction. In 6 (50%) out of 12 reviewed works all contacts are the same. In another 5 (41.7%) papers contacts are divided into 3 categories: close, permanent (family, friends) and casual, not close (contacts on the street, work, school). In 1 (8.3%) article, the division of interactions by types is more complex.

For example, in a study conducted by J. Whitman et al., the interactions are divided into two levels: intra-cohort (strong ties, high probability of transmission) and inter-cohort (weak ties, rare cases of virus transmission, number of ties is smaller) [19]. This allowed us to account for the presence of clusters in the distribution of contacts and to reproduce the repetitive behavior of peaks in disease spread with significant stochasticity. Using this model, the researchers studied the behavior of the reproductive number at different values of the initial immune profile of the population, as well as the dynamics of the infection time series when the population size and contact matrix change.

A study by X. Guo et al. presented a multilevel model of the relationship between disease transmission and emotional stress in society [20]. In this paper, two independent networks of contacts are superimposed. Each node represents some group of people, infection and information exchange occurs through the edges of these nodes. Each node, in turn, models a set of individuals in each node, which increases the accuracy of the results.

In the study conducted by N.N. Chung et al. presents a contact network consisting of a set of overlapping networks (households, dormitories, workplaces, dynamic crowd network, dynamic social gathering network) [21].

Agent-based modeling based on the construction of AP without taking into account the spatial localization and demographic properties of agents makes it possible to solve a fairly wide range of problems without additional complication of the model. This approach was used to study the influence of such factors as population size, immunity parameters, the number and nature of agent relationships, and population density on the modeling results. This approach also allows us to analyze quarantine and testing strategies, the nature of repeated peaks of incidence, the dynamics of mutant infections, and the role of super-spreaders (agents with a large number of linkages).

The lack of detailing the properties of agents when creating the AP allows us to simplify the computational model and increase its interpretability. At the same time, the main limitations of the AP considered in this section are the lack of the possibility of introducing adjustable clustering (for example, separating pensioners into a separate group) and taking into account the behavior of the population, as well as the inappropriateness of such models to study the physical impact of social interactions.

Approaches to creating an AP that takes into account properties of agents without considering locations (64 studies)

APs in which agents with demographic, biological, and social properties interact with each other in an unstructured space are the most common in agent-based modeling. Many authors consider this type of AP to be optimal from the point of view of accuracy/performance balance. This approach is also popular due to the fact that high computational efficiency allows the agents to be endowed with an extensive set of parameters.

The construction of a network of contacts in the considered type of AP is often based on the creation of 4 main layers: households, work, schools and kindergartens, and society. In more complex models, up to 30 layers can be overlaid.

The considered agent-based models based on the formation of AP, taking into account the properties of agents without taking into account locations, according to the nature of the realization of social ties were distributed as follows:

• Uniform contact— 11 (17.2%) publications;
• Close/long distance contact — 1 (1.5%);
• Three or more types of contact — 52 (81.3%).

The most common agent characteristics include age (64/64) and sex (9/64). Age groups may differ in the likelihood of infection and the development of more severe cases of disease. The age structure of the population also affects the properties of contact networks between agents. For example, in models with homogeneous contacts, the network of interactions is built based on age-specific contact matrices [22, 23]. Work contacts may be excluded for the older generation, and some models construct additional blocks of contact networks for elderly care facilities [24-30].

The number and nature of contacts between agents may depend on the agent's occupation/profession. In the simplest case, professions such as teacher and hospital employee are modeled. Such an approach allows modeling elements of temporal dynamics of agents' interaction, e.g., five-day working day, possibility of vacation and skipping school/work, division of contact networks into daytime (school, work) and evening/nighttime (home, community) ones.

About 20% of the publications reviewed in this section use the Covasim environment for AP construction and modeling [10]. In its basic version, Covasim is an open-source modeling environment adapted to study the dynamics of the COVID-19 pandemic. The AP embedded in Covasim represents a set of people, each with attributes such as age, gender, and social status (Figure 5). In modeling the spread of infection, the model takes into account the frequency of contacts, the infectiousness of the virus, and the susceptibility of agents.

 

Fig. 5. Inter-agent interactions under the assumption that agents do have properties. Constant (solid lines) and dynamic (dashed lines) contact networks are modelled.

 

Using the open source agent-based modeling environment Covasim, researchers can explore different epidemic scenarios by changing infection parameters and modeling various interventions such as social distancing, isolation, testing, contact tracing, and vaccination campaigns. In a study conducted by A. Cattaneo et al., the Covasim environment was used to evaluate the effectiveness and optimization of a COVID-19 vaccination campaign in the Italian region of Lombardy [31]. The age structure of the population and the household characteristics were matched with data from the Italian National Institute of Statistics, while the rest of the contact network variables were constructed based on the default parameters embedded in Covasim. Different levels of constraints were modeled by reducing the number of contacts in the school, work and social interaction strata, and by varying the probability of transmission between household members. The Covasim environment also allows for the specification and tracking of dynamic characteristics of agent immunity. For example, vaccination, as well as disease, affects the dynamics of neutralizing antibodies and the level of protection of agents; cross-immunity with a given degree of effectiveness is realized when different strains of the virus are present in the population. In the study of A. Cattaneo et al., the Covasim model showed results consistent with the registered cases of COVID-19 infection, detection and mortality, the most effective vaccination strategy was determined and age priorities for vaccination were proposed [31].

In general, agent-based modeling on AP, which takes into account the properties of agents without taking into account their locations, is used to study the development of an epidemic taking into account various demographic data, as well as to assess the effects of diseases on public health and the economy. In particular, such modeling makes it possible to assess the effectiveness of quarantine measures, analyze vaccination scenarios (including those targeting different age groups of the population), calculate the economic cost of introducing restrictive measures, and build population immunity.

One of the main limitations of this type of AP is the simplified representation of the network of contacts [32], as well as the idealization of individuals' activities during the day [33]. The authors also emphasize the potential importance of additional properties of agents, which are not taken into account in this approach to modeling [24, 34].

Approaches to agent location-aware and agent property-aware AP (12 studies)

The main purpose of AP modeling with and without taking into account the spatial movements of agents is to reflect both the mobility of agents and the spatial dynamics of their movements during the spread of an epidemic.

The most common tool for this approach is the NetLogo software. In this environment, a map of a closed space is represented either by a coordinate grid or by a set of cells, and agents move randomly across the map or according to specified movement patterns (Fig. 6) [35-37]. Infection in this type of representation is possible if the agents (infected and susceptible) collide, converge to some threshold distance, or fall into one cell.

 

Fig. 6. Representation of an artificial population accounting for the movement of identical agents. A contact is defined as a collision, approaching a critical distance, and/or agents entering the same cell.

 

In the agent-based models we have considered, based on the formation of AP with and without taking into account the location of agents, social ties were analyzed as follows:

• Uniform contact — 6 (50%) publications;
• Close/long distance contact — 4 (34%);
• Three or more types of contact — 2 (16%).

A good example of this approach is shown in the study by T. Daghriri et al., in which several ways of distancing were modeled and the movements of agents resulting from different scenarios were visually represented [35]. The model took into account the possibility of a part of the agents not respecting the distancing. The authors showed the importance of compliance with restrictive measures and depicted the correlation between the strictness of the social distancing policy and the spread of the disease.

The two main models describing the movement of agents in the environment are random walks and the gravity model, according to which the strength of interaction (intensity of flows) depends on the importance (magnitude) of objects and the distance between them. For example, the study conducted by N. Kishore et al. showed that a densely populated center has a higher probability of being visited by agents [38].

The main goals of research in this approach are to study distancing strategies, the effectiveness of restrictive quarantine measures, the role of geographical factors in the spread of disease, and the role of super-spreaders. Such modeling also allows direct tracking of contacts of individuals in a population. However, it is not possible to model the implementation of anti-epidemic measures in different age and social groups of the population.

Approaches to creating an AP that takes into account the location and properties of the agents (56 studies)

When modeling with both geographic and demographic data, researchers try to achieve the closest approximation to the real population, with the goal of creating a digital twin. Typically, contact networks are divided into households, schools, workspace, and community, and geographic features are taken into account in two ways: modeling agents' movements on a map or capturing the location of buildings and determining the probability of agents visiting them. However, if in the group of APs that take into account the location of agents without taking into account their properties, the more common was the mapping of terrain, then in the works that take into account both the properties of agents and the properties of places, the division of the model space into conditional locations in which an agent can be located was more often used in the creation of APs (Fig. 7).

 

Fig. 7. Artificial population taking into account the location and characteristics of agents. It is possible to overlay a network of contacts on a map or to simulate the movements and contacts of agents.

 

The most common framework for this type of model is FRED (a Framework for Reconstructing Epidemic Dynamics) [39]. FRED uses synthetic populations based on census data that reflect the demographic and geographic heterogeneity of the population. Each agent has associated demographic and socioeconomic information (e.g., age, gender, race, family income). Race, along with sex and age, can be used to account for known disease prevalence. Households, educational and health institutions, places of work, and some other locations are georeferenced to a spatial grid of coordinates (at 1 km resolution). When calculating the probability of visiting different geographic locations, the agent's household income is taken into account. One of the features of this model is the ability to take into account the dynamic demography of agents, including aging, fertility and mortality. Works [40-43] have been performed on the basis of this model. Currently, FRED continues to be actively used to study seasonal influenza.

M.G. Krauland et al. studied the effect of a decrease in population immunity caused by the restriction of virus activity on its dynamics in subsequent years [43]. Modeling was conducted for a population representing Allegheny County (Pennsylvania, USA) with a population of about 1.2 million. This county includes both urban and suburban areas and is large enough to investigate influenza patterns. According to the results, a decrease in the incidence rate in the first season will lead to an increase in the incidence rate in the second season. Compensating for the decline in population immunity may help to increase vaccination. Depending on cross-immunity from previous infection and the transmissibility of the strain, the incidence rate could increase by up to 50%.

Many of the publications reviewed in this section describe complicated models where additional parameters have been added to the basic version of the AP. In particular, A. Truszkowska et al. modified the basic version of the model by adding the division of the able-bodied population into spheres of activity [44]. This allowed the model to reflect the complex structure of employment. And in the study conducted by C. Fosco et al., the labor force was divided into 4 groups according to different mobility in case of quarantine measures [45].

A number of works paid more attention to the division of the day into time segments. In 24 models, the temporal characteristics of agents' mobility were taken into account (taking into account the schedule, division of the day).

The goals of approaches that take into account both agent and location properties include:

• management decision analysis;
• finding the optimal approach to implementing non-pharmaceutical interventions;
• study of infection spread using GPS;
• studying the spread of the pathogen in its early stages;
• studying the distribution of different strains;
• modeling contact tracing and virus transmission;
• studying the spread of the virus in different countries/cities;
• exploring vaccination strategies;
• studying the protection of the population depending on the past season.

In generating this type of AP, model developers often resort to various simplifications to allow for the inclusion of additional characteristics that they consider crucial [46]. Some assumptions exceed the current understanding of the mechanisms of epidemic development, allowing them to be included in the study only in an approximate form [47]. It is common practice to use updated real-world data as the basis for the creation of an AP-digital twin, which is then projected onto a sample of smaller size than the general population. Even if the sample replicates the structure of the real population, the results obtained for it may not fully reflect the situation in the real population [48].

Increasing complexity of AP formation

When creating a realistic population for epidemiologic studies, an extensive set of parameters is required, each of which cannot be taken into account at the moment. Basic versions of models allow describing the epidemiologic process in a general way and investigating regularities and trends in the dynamics of epidemics.

In order to make it more plausible, some authors have resorted to complicating the AP by introducing the following parameters:

• seasonality;
• comorbidities;
• dynamic immunity;
• ethnicity;
• profits;
• transport flows.

The heterogeneity of the population in terms of the susceptibility of individuals to the virus and the severity of the disease can be accounted for by a co-morbidity factor. In the simplest version, co-morbidities can be taken into account thanks to the binary parameter (present or absent) [28]. In a more complex version, by introducing an additional module for calculating the risk factor, it is possible to take into account both specific diseases (type 1 and type 2 diabetes, hypertension, cardiovascular diseases, etc.) and risk factors related to lifestyle (smoking, physical activity, increased body mass index, etc.) [49].

In certain studies, dynamic immunity modeling has been performed. A popular framework for accounting for immunity has been the Covasim model [50–52], which provides the possibility of dynamically changing the values of the level of specific immune defense for each agent and the population as a whole.

Seasonality can affect both the properties of the pathogen (mainly used in modeling seasonal influenza) and other parameters (effect of average daily temperature on susceptibility, effect of season on the contact network with sex distribution, etc.). [43, 53–58].

If appropriate data are available, it is possible to add sociological parameters of agents — income level and ethnicity, and these characteristics can be reflected in the model in different ways. In the study conducted by M.D. Patel et al., people of different nationalities had different susceptibility to the virus and tolerated the disease differently [59]. In the study conducted by C. Fosco et al., income level influenced the ability of workers to stay at home during the epidemic [45]. In the study conducted by M. Thakur et al. income was directly correlated with decreased vaccination rates [60].

Modeling of transport flows within the AP was used in 15 (10%) papers, 8 of which considered geographic and demographic population data, 7 — only demographic data.

Representation of transport was possible in the form of:

• an additional random network of contacts;
• more transportation stops/blocks;
• addition of common agent routing.
• Some researchers have resorted to dividing transportation into modes:
• automobiles, hitchhiking, public transport, walking, etc. (with the possibility of getting infected only in automobiles and public transportation) [25];
• metro, bus, shuttle bus [61].

Conclusion

AP formation is a key point in the construction of predictive agent-based models. The use of ABM allows us to consider the population at the level of individual representatives, which opens new opportunities for studying the development of epidemics and analyzing measures to prevent the spread of infection.

In our review, based on the analysis of 144 original studies, we consider 4 variants of AP construction with different degrees of detail. We intentionally used the PubMed database exclusively for the literature search because it is focused on biomedical research, including epidemiology. This choice allowed us to analyze the main publications published in ranked peer-reviewed journals in the field of interest, but it is possible that some part of the available publications was not considered. The review also considered articles published since the beginning of the COVID-19 pandemic. This allowed us to analyze the most relevant cross-section of papers, focusing on the demanded solutions in AP formation, while the review did not include the previously published EpiSimS [62] and TRANSIMS models [63].

It should be noted that all the considered variants of AP construction turned out to be suitable for solving the list of tasks in the field of infectious disease epidemiology stated by the developers. The limitations of the present study are dictated by the impossibility of experimental confirmation of the success of the implementation of the presented ABM to achieve the goals and objectives in the reviewed studies. In most cases, there is no possibility to critically conceptualize the model due to the availability of a general, often superficial description of its device given in the publication and the lack of access to the source code of the model. The selected literature was analyzed largely on the basis of the authors' evaluation of the results of the papers. In most cases, the authors do not provide an analysis of the sensitivity of the result to the parameters of the modeled pathogen and AP. Such analysis is an important feature of complex models and can show the real importance of parameters, and this review revealed a systematic shortcoming of a large part of the analyzed papers.

Among the identified limitations in AP creation, the most significant are the insufficiency and anachronism of real demographic and statistical data required for further accounting in the model. Works that take into account the properties of agents in the AP, as a rule, rely on census data or sociological surveys, which do not always have the required detail. Models that incorporate the movement of agents on a city map use information from specialized applications, databases and mapping services such as Google Maps and OpenStreetMap. Obtaining this data and incorporating it into the model can be challenging, so simplified models based on assumptions about agent behavior and interactions were used in some cases.

The use of complex and diverse real demographic and statistical data is possible when studying small groups (at the level of a room, building), but for larger studies, the computational complexity in case of increasing the number of parameters or population size may exceed the technical capabilities of the calculation and lead to unreliable or uninterpretable results.

Further research on the creation and use of AP in agent-based modeling can be focused on optimizing methods of model parameterization and finding a balance between model detail and interpretability to achieve maximum accuracy and precision of results. When creating a AP, it is important to consider the factors that can be targeted for control. This will improve the quality of public health decision-making and increase the effectiveness of epidemic response.

About the authors

Irina I. Maslova

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0009-0000-0849-9123

student

Россия, Moscow

Aleksandr I. Manolov

Research Institute of Systems Biology and Medicine

Author for correspondence.
Email: paraslonic@gmail.com
ORCID iD: 0000-0003-3912-429X

Cand. Sci. (Biol.), researcher

Россия, Moscow

Oksana E. Glushchenko

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0000-0002-2028-3066

junior researcher

Россия, Moscow

Ivan E. Kozlov

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0009-0007-2437-5527

research assistant

Россия, Moscow

Vera I. Tsurkis

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0009-0001-5140-0990

student

Россия, Moscow

Nikolay S. Popov

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0009-0002-6450-8594

student

Россия, Moscow

Andrey E. Samoilov

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0000-0001-8284-3164

researcher

Россия, Moscow

Alexandr N. Lukashev

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0000-0001-7365-0352

D. Sci. (Biol.), Corresponding member of RAS, chief scientist

Россия, Moscow

Elena N. Ilina

Research Institute of Systems Biology and Medicine

Email: paraslonic@gmail.com
ORCID iD: 0000-0003-0130-5079

D. Sci. (Biol.), Сorresponding member of RAS, chief scientist, Head, Laboratory for mathematical biology and bioinformatics

Россия, Moscow

References

Supplementary files