Ограничения в создании искусственных популяций в агентном моделировании эпидемий: систематический обзор
- Авторы: Маслова И.И.1, Манолов А.И.1, Глущенко О.Е.1, Козлов И.Е.1, Цуркис В.И.1, Попов Н.С.1, Самойлов А.Е.1, Лукашев А.Н.1, Ильина Е.Н.1
-
Учреждения:
- Научно-исследовательский институт системной биологии и медицины
- Выпуск: Том 101, № 4 (2024)
- Страницы: 530-545
- Раздел: ОБЗОРЫ
- URL: https://microbiol.crie.ru/jour/article/view/18491
- DOI: https://doi.org/10.36233/0372-9311-467
- EDN: https://elibrary.ru/goxztx
- ID: 18491
Цитировать
Аннотация
Введение. Ключевым этапом агентного моделирования эпидемий, позволяющим исследователям учитывать индивидуальные особенности людей, является создание искусственной популяции. Основная сложность этой процедуры — поиск баланса между подробностью описания популяции и вычислительной эффективностью расчётов.
Цели и задачи обзора: критически проанализировать и обобщить актуальные данные о способах создания искусственных популяций; оценить ограничения и преимущества имеющихся подходов при решении различных задач в эпидемиологии.
Материалы и методы. Проведён анализ источников литературы, посвящённых агентному моделированию. Анализ сфокусирован на алгоритмах создания искусственной популяции с заданным уровнем детализации для моделирования респираторных инфекций человека.
Результаты. Обобщены подходы к созданию искусственных популяций. Выявлены основные принципы реализации взаимодействия между агентами: с помощью сетей контактов между агентами и на основе учёта перемещения агентов между локациями. Первый подход является наиболее эффективным для вычислений и простым; второй подход позволяет лучше учитывать изменение поведения агентов в ходе развития эпидемического процесса.
Заключение. Агентное моделирование — оптимальный инструмент при выборе наилучшего сценария проведения противоэпидемических мероприятий и исследовании роли индивидуальных особенностей людей в развитии эпидемий. При создании искусственной популяции важно включать в модель факторы, на которые может быть направлен контроль. Существенным ограничением является отсутствие фактологических данных о структуре популяции, однако его можно преодолеть за счёт привлечения косвенных данных.
Полный текст
Введение
С начала 2000-х гг. человечество столкнулось с рядом вирусных эпидемий, включая тяжёлый острый респираторный синдром (ТОРС, 2002–2003 гг.), грипп A(H1N1)-California (свиной грипп) (2009 г.), Ближневосточный респираторный синдром (MERS, 2012 г.), вспышки лихорадки Эбола (с 2014 по 2016 г.), лихорадки Зика (2015–2016 гг.) и, наконец, пандемию COVID-19, вызванную новым коронавирусом SARS-CoV-2 (с 2019 г. по настоящее время). Пандемия COVID-19 вызвала интерес специалистов в области эпидемиологии и здравоохранения к использованию вычислительных средств для прогнозирования развития эпидемий и подбора оптимальных противоэпидемических мер. К этим средствам относятся методы машинного обучения и компьютерные эпидемиологические модели.
Компьютерное моделирование в эпидемиологии предназначено для воспроизведения динамики распространения инфекционного заболевания с учётом демографических характеристик населения [1–3], структуры сети контактов [4] и информации о стратегиях вмешательства [5, 6]. Эти модели представляют собой виртуальную лабораторию, позволяющую изучать гипотетические сценарии, оценивать эффективность различных мер и предвидеть траектории развития вспышек.
Численное решение обыкновенных дифференциальных уравнений и агентно-ориентированное моделирование (АОМ) — два наиболее распространённых подхода к моделированию в эпидемиологии [7, 8]. К первому подходу относятся различные компартментные модели, например, модель «восприимчивый–инфицированный–выздоровевший» [9] и её модификации; ко второму — агентные модели, которые учитывают неоднородность популяции за счёт моделирования действий и взаимодействий отдельных агентов (людей) внутри неё [3, 4, 10].
Агентные модели рассматривают каждого человека как автономного агента, обладающего характеристиками, определяющими его поведение и социальные взаимодействия. Смысловые блоки, на которые можно разделить любую синтетическую популяцию, представлены на рис. 1.
Рис. 1. Искусственная популяция включает агентов с различными демографическими характеристиками (Блок А). Этим агентам назначаются некоторые обязанности, которые они должны выполнять в определённых местах и в определённое время. Так образуется сеть, которая соединяет агентов с локациями в течение дня, создавая сеть человек–локация (Блок В). Сеть контактов человек–человек (Блок Б) разрабатывается на основе взаимодействий, полученных на основе графа человек–локация.
Fig. 1. The artificial population consists of agents with different demographic characteristics (block A). These agents are assigned specific tasks to perform at specific locations and times. This determines a network that connects agents to locations throughout the day, creating a person-location network (Block В). The person-to-person contact network (Block Б ) is developed based on the interactions obtained from the person-to-location graph.
Агентно-ориентированный подход применим для изучения противоэпидемических мер [11–13], оценки эффективности воздействий на различные группы населения [14] и проведения анализа чувствительности результатов моделирования к изменениям в значениях параметров [15]. Основные цели применения АОМ в интересах общественного здравоохранения заключаются в анализе и прогнозировании последствий предполагаемых вмешательств для здоровья населения с учётом аспектов сложной социальной структуры. Модели, построенные на основе АОМ, помогают понять основные механизмы, определяющие динамику и результаты протекания эпидемий. АОМ могут быть использованы для виртуальных экспериментов, исследующих различные стратегии вмешательств, и других мероприятий по снижению заболеваемости среди населения [16]. Всё это делает их важным инструментом исследований и обучения специалистов в области общественного здравоохранения.
Основная сложность использования АОМ как инструмента социальных, политических и экономических исследований заключается в грамотном сопоставлении цели моделирования и степени детализации модели [17]. Недостатком АОМ может стать избыточная подробность, которая усложняет общую задачу моделирования и приводит к созданию чрезмерно сложных моделей с избыточными параметрами, которые не вносят существенного вклада в результаты моделирования [18].
Поиск баланса в выборе учитываемых параметров и сложности при создании искусственной популяции (ИП) для АОМ — открытый вопрос, стоящий перед исследователями. Настоящий систематический обзор имеет целью выявить наиболее распространённые подходы к созданию ИП при агентном моделировании и конкретизировать их ограничения.
Материалы и методы
Данный систематический обзор основан на рекомендациях PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses). Систематический поиск литературы проводили с использованием базы данных PubMed. Поиск осуществляли с использованием ключевых слов: «agent-based» AND «epidemiology». Рассмотрены полнотекстовые статьи, опубликованные в 2020–2024 гг. В ходе первичной оценки были отобраны исследования, использующие агентное моделирование, изучающие респираторные вирусные инфекции и имеющие достаточно подробное описание модели (рис. 2).
Рис. 2. Схема отбора публикаций для систематического обзора.
Fig. 2. Publication selection scheme for the systematic review.
Из исследования были исключены работы, изучающие поведение вируса в отдельном организме, а также исследования, посвящённые моделированию инфекций животных.
Согласно методике поиска было отобрано 144 исследования, опубликованных в международных журналах на английском языке, которые использовались для дальнейшего анализа. Русскоязычных публикаций, удовлетворяющих критериям отбора, не обнаружено. Отобранные публикации были систематизированы согласно способам задания ИП по критериям «локация» (учёт пространства) и «свойства агента». К свойствам агента были отнесены такие характеристики, как пол, возраст, сфера деятельности, этническая принадлежность, доход и подобные — т.е. характеристики, определяемые на основе демографических и статистических данных. Мы считали, что модель учитывает локации, если вероятность передачи инфекции зависела от пространственного положения агента. Такое свойство модели может быть реализовано как за счёт отслеживания координат каждого агента в моделируемом пространстве, так и с помощью моделирования отдельных пространственных сущностей (например, «магазин», «школа»), в которых могут размещаться агенты.
Результаты
В 2020–2024 гг. наибольший интерес исследователей был направлен на моделирование распространения в популяции вируса SARS-CoV-2 — возбудителя COVID-19: 129 (89%) работ из 144 отобранных моделировали распространение данного вируса, 10 (11%) работ — распространение вируса гриппа. В ряде работ исследователи представляли свои модели как подходящие для изучения нескольких респираторных заболеваний (табл. 1).
Таблица 1. Распределение статей по моделируемому возбудителю
Table 1. Distribution of the articles according to the pathogen
Патоген | Pathogen | Количество публикаций Publication amount | |
n | % | |
SARS-CoV-2 | 129 | 89 |
Вирус гриппа | Influenza | 10 | 6,9 |
Вирус кори | Measles | 1 | 0,7 |
MERS-CoV | 1 | 0,7 |
Неуточнённые респираторные заболевания Unspecified respiratory diseases | 4 | 2,7 |
Для систематизации типов ИП, используемых в моделях, проанализировали наличие свойств агентов и учёт их локации. На рис. 3 приведено распределение рассмотренных в обзоре публикаций согласно типу описываемых в них ИП.
Рис. 3. Распределение публикаций по типам ИП. *При этом агенты могут быть наделены индивидуальным уровнем защиты от патогена (иммунитета) и уровнем вирусной нагрузки. **В эту группу также включены работы, которые учитывают пространственное расположение зданий и/или агентов.
Fig. 3. Distribution of publications by artificial population type. *Аt the same time, agents can be endowed with an individual level of protection against the pathogen (immunity) and the level of viral load. **Тhis group also includes papers that consider the spatial location of buildings and/or agents.
Можно выделить 4 варианта построения ИП, исходя из комбинаций наличия и отсутствия учёта свойств агентов и учёта локаций.
Подходы к созданию ИП без учёта локации и свойств агента (12 статей)
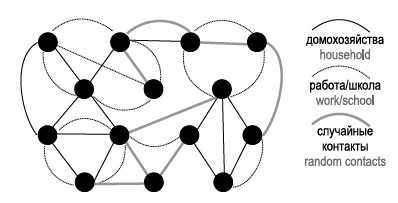
ИП без учёта пространственной локализации и демографических свойств агентов представляет собой граф — сеть контактирующих агентов (рис. 4). Стохастичность таких моделей создаётся за счёт генерации индивидуальных наборов связей у каждого узла (агента) на основе заданных вероятностных распределений числа контактов.
Рис. 4. Сеть контактов без учёта свойств агентов и пространственных характеристик. Каждый узел — агент, ребра между узлами — контакт на одном из слоёв.
Fig. 4. A network of contacts without considering the properties of agents and spatial characteristics is illustrated. Each node represents an agent, and the edges between nodes indicate a contact on one of the layers.
При этом контакты или социальные связи могут быть одинаковыми или различаться по силе и периодичности взаимодействия. В 6 (50%) из 12 рассмотренных работ все контакты являются одинаковыми. Ещё в 5 (41,7%) работах контакты разделены на 3 категории: близкие, постоянные (семья, друзья) и случайные, не близкие (контакты на улице, работа, школа). В 1 (8,3%) статье разделение взаимодействий по типам происходит более сложным образом.
Например, в статье J. Whitman и соавт. взаимодействия разделены на два уровня: внутрикогортные (сильные связи, высокая вероятность передачи вируса) и межкогортные (слабые связи, редкие случаи передачи вируса, количество связей меньше) [19]. Это позволило учесть наличие кластеров в распределении контактов и воспроизвести повторяющееся поведение пиков при распространении заболевания со значительной стохастичностью. С помощью этой модели исследователи изучили поведение репродуктивного числа при различных значениях начального иммунного профиля популяции, а также динамику временнóго ряда заражения при изменении численности и контактной матрицы популяции.
В статье X. Guo и соавт. представлена многоуровневая модель связи между передачей заболевания и эмоциональным напряжением в обществе [20]. В данной работе происходит наложение двух независимых сетей контактов. Каждый узел представляет некоторую группу людей, заражение и обмен информацией происходит через рёбра данных узлов. В каждом узле, в свою очередь, моделируется набор индивидов, что повышает точность результатов.
В работе N.N. Chung и соавт. представлена сеть контактов, состоящая из множества перекрывающихся сетей (домохозяйства, общежития, рабочие места, динамическая сеть толпы, динамическая сеть общественных собраний) [21].
Агентное моделирование на основе построения ИП без учёта пространственной локализации и демографических свойств агентов даёт возможность решать достаточно широкий спектр задач без дополнительного усложнения модели. Данный подход был использован для исследования влияния на результат моделирования таких факторов, как размер популяции, параметры иммунитета, количество и характер связей агентов, плотность населения. Этот подход также позволяет проводить анализ стратегий карантина и тестирования, исследовать характер повторных пиков заболеваемости, динамику распространения мутирующих инфекций, роль суперраспространителей (агентов с большим количеством связей).
Отсутствие детализации свойств агентов при создании ИП позволяет облегчить вычислительную модель и повысить её интерпретируемость. При этом основным ограничением ИП, рассмотренных в данном разделе, является отсутствие возможности введения настраиваемой кластеризации (например, выделение пенсионеров в отдельную группу) и учёта поведения населения, а также неприспособленность таких моделей к изучению влияния общественных взаимодействий.
Подходы к созданию ИП, учитывающей свойства агентов без учёта локаций (64 статьи)
ИП, в которых агенты, имеющие демографические, биологические, социальные свойства, взаимодействуют друг с другом в неструктурированном пространстве, наиболее распространены в агентном моделировании. Именно такой тип ИП многие авторы считают оптимальным с точки зрения баланса точность/производительность. Данный подход популярен также благодаря тому, что высокая вычислительная эффективность позволяет наделить агентов обширным набором параметров.
Построение сети контактов в рассматриваемом типе ИП зачастую основывается на создании 4 основных слоев: домохозяйства, работа, школы и детские сады, общество. В более сложных моделях возможно наложение до 30 слоев.
Рассмотренные нами агентные модели, основанные на формировании ИП, учитывающей свойства агентов без учёта локаций, согласно характеру реализации социальных связей распределялись следующим образом:
- однотипные контакты — 11 (17,2%) статей;
- разделение на близкие/дальние контакты — 1 (1,5%);
- разделение на 3 и более типов контактов — 52 (81,3%).
К наиболее распространённым свойствам агентов относятся возраст (64/64) и пол (9/64). Возрастные группы могут различаться вероятностью заражения и развития более тяжёлых случаев заболевания. Возрастная структура популяции также влияет на свойства сетей контактов между агентами. Так, в моделях с однотипными контактами сеть взаимодействий строится на основе возрастных матриц контактов [22, 23]. Для старшего поколения могут быть исключены рабочие контакты, а в некоторых моделях строятся дополнительные блоки сетей контактов для учреждений по уходу за пожилыми людьми [24–30].
Количество и характер контактов между агентами могут зависеть от рода деятельности/профессии агента. В простейшем случае моделируются такие профессии, как учитель и сотрудник больницы. Подобный подход допускает моделирование элементов временнóй динамики взаимодействия агентов, например, пятидневного рабочего дня, возможности отпуска и пропуска школы/работы, разделения сетей контактов на дневные (школа, работа) и вечерние/ночные (дом, сообщество).
Около 20% публикаций, рассматриваемых в этом разделе, используют для построения ИП и моделирования среду Covasim [10]. В базовой версии Covasim — это среда моделирования с открытым исходным кодом, адаптированная для изучения динамики пандемии COVID-19. ИП, заложенная в Covasim, представляет собой набор людей, каждый из которых обладает такими атрибутами, как возраст, пол и социальный статус (рис. 5). При моделировании распространения инфекции модель учитывает частоту контактов, контагиозность вируса и восприимчивость агентов.
Рис. 5. Межагентные взаимодействия при условии наличия у агентов заданных свойств. Моделируются постоянные (сплошные линии) и динамические (пунктирные линии) сети контактов.
Fig. 5. Inter-agent interactions under the assumption that agents do have properties. Constant (solid lines) and dynamic (dashed lines) contact networks are modelled.
Используя открытую среду агентного моделирования Covasim, исследователи могут изучать различные сценарии развития эпидемического процесса, изменяя параметры инфекции, а также моделируя различные вмешательства, такие как социальное дистанцирование, изоляция, тестирование, отслеживание контактов и кампании вакцинации. В статье A. Cattaneo и соавт. среда Covasim использована для оценки эффективности и оптимизации кампании по вакцинации от COVID-19 в итальянском регионе Ломбардия [31]. Возрастная структура населения и характеристики домохозяйств соответствовали данным Итальянского национального института статистики, остальные переменные сети контактов были построены на основе параметров, заложенных в Covasim по умолчанию. Моделирование различных уровней ограничений было реализовано посредством снижения количества контактов в школьном, рабочем и общественном слоях взаимодействий, а также посредством изменения вероятности передачи вируса между членами домохозяйства. Среда Covasim позволяет также задавать и отслеживать динамические характеристики иммунитета агентов. Так, вакцинация, как и перенесённое заболевание, влияет на динамику нейтрализующих антител и уровень защиты агентов; при наличии в популяции различных штаммов вируса реализуется перекрёстный иммунитет с задаваемой степенью эффективности. В работе A. Cattaneo и соавт. модель Covasim показала результаты, согласующиеся с зарегистрированными случаями заражения, выявления и смертности от COVID-19, была определена наиболее эффективная стратегия вакцинации и предложены возрастные приоритеты при введении вакцинации [31].
В целом агентное моделирование на ИП, учитывающей свойства агентов без учёта их локаций, используется для изучения развития эпидемии с учётом различных демографических данных, а также для оценки последствий заболеваний на здоровье населения и экономику. В частности, такое моделирование позволяет проводить оценку эффективности карантинных мероприятий, анализ сценариев вакцинации (в том числе направленных на разные возрастные группы населения), расчёт экономической стоимости введения ограничительных мер, формирование популяционного иммунитета.
Одними из главных ограничений при создании ИП данного типа являются упрощённое представление сети контактов [32], а также идеализация деятельности индивидов в течение дня [33]. Авторы также подчёркивают потенциальную важность дополнительных свойств агентов, которые не учитываются при таком подходе к моделированию [24, 34].
Подходы к созданию ИП с учётом местоположения агентов и без учёта их свойств (12 статей)
Основная цель моделирования ИП с учётом пространственных перемещений агентов и без учёта их свойств — отражение и мобильности агентов, и пространственной динамики их перемещений при распространении эпидемии.
Наиболее распространённый инструмент для такого подхода — программное обеспечение «NetLogo». В этой среде карта замкнутого пространства представляется либо координатной сеткой, либо набором ячеек, а агенты перемещаются по карте случайно или согласно заданным законам перемещения (рис. 6) [35–37]. Заражение при данном типе представления возможно в том случае, если происходит столкновение, сближение агентов (заражённого и уязвимого) на некоторое пороговое расстояние или попадание агентов в одну ячейку.
Рис. 6. Представление ИП, учитывающей перемещение идентичных агентов. Контактом считается столкновение, сближение на критическое расстояние и/или попадание агентов в одну ячейку.
Fig. 6. Representation of an artificial population accounting for the movement of identical agents. A contact is defined as a collision, approaching a critical distance, and/or agents entering the same cell.
В рассмотренных нами агентных моделях, основанных на формировании ИП с учётом местоположения агентов и без учёта их свойств, социальные связи анализировали следующим образом:
- контакт при сближении — 6 (50%) статей;
- разделение на близкие/дальние контакты — 4 (34%);
- разделение на 3 и более типов контактов — 2 (16%).
Наглядным примером такого подхода является работа T. Daghriri и соавт., в который были смоделированы несколько способов дистанцирования и визуально представлены перемещения агентов, полученные в результате различных сценариев [35]. Модель учитывала возможность части агентов не соблюдать дистанцирование. Авторы показали важность соблюдения ограничительных мер и отобразили корреляцию между строгостью политики социального дистанцирования и распространением заболевания.
Две основные модели, описывающие перемещение агентов в среде, — случайные блуждания и гравитационная модель, согласно которой сила взаимодействия (интенсивность потоков) зависит от значимости (величины) объектов и расстояния между ними. Например, в работе N. Kishore и соавт. показано, что густонаселённый центр имеет более высокую вероятность посещения агентами [38].
Основными целями исследования при подобном подходе является изучение стратегий дистанцирования, эффективности ограничительных карантинных мер, роли географических факторов в распространении болезни, а также роли суперраспространителей. Такое моделирование позволяет также напрямую отслеживать контакты индивидов в популяции. При этом отсутствует возможность моделирования проведения противоэпидемических мероприятий в разных возрастных и социальных группах населения.
Подходы к созданию ИП, учитывающей локацию агентов и их свойства (56 статей)
При моделировании с учётом как географических, так и демографических данных исследователи стараются достичь максимальной приближенности к реальной популяции, ставится цель создания «цифрового двойника». Обычно сети контактов разделяются на домохозяйства, школы, рабочее пространство и сообщество, а географические особенности учитываются двумя способами: моделированием перемещений агентов по карте или фиксированием местоположения зданий и определением вероятности их посещения агентами. Однако если в группе ИП, учитывающих локацию агентов без учёта их свойств, более распространённым являлось картирование местности, то в работах, учитывающих и свойства агентов, и свойства мест, при создании ИП чаще применялось разделение модельного пространства на условные локации, в которых может находиться агент (рис. 7).
Рис. 7. ИП с учётом локации и свойств агентов. Возможно наложение сети контактов на карту или моделирование перемещений и сближений агентов.
Fig. 7. Artificial population taking into account the location and characteristics of agents. It is possible to overlay a network of contacts on a map or to simulate the movements and contacts of agents.
Самой распространённой основой для данного типа моделей стала система FRED (a Framework for Reconstructing Epidemic Dynamics) [39]. FRED использует синтетические группы населения, основанные на данных переписи населения, которые отражают демографическую и географическую неоднородность населения. У каждого агента есть связанная демографическая и социально-экономическая информация (например, возраст, пол, раса, доход семьи). Раса, наряду с полом и возрастом, может использоваться для учёта известной распространённости заболеваний. Домохозяйства, учебные и лечебные учреждения, места работы и некоторые другие локации имеют привязку к пространственной сетке координат (с разрешением в 1 км). При расчёте вероятности посещения различных географических локаций учитывается доход семьи агента. Одной из особенностей данной модели является возможность учёта динамической демографии агентов, включая старение, рождаемость и смертность. На основе данной модели были выполнены работы [40–43]. В настоящее время FRED продолжает активно использоваться для изучения сезонного гриппа.
M.G. Krauland и соавт. изучали влияние снижения иммунитета населения, вызванное ограничением активности вируса, на его динамику в последующие годы [43]. Моделирование проводилось для населения, представляющего округ Аллегейни (Пенсильвания, США) с населением около 1,2 млн человек. Данный округ включает в себя как городские, так и пригородные районы, и он достаточно велик, чтобы исследовать закономерности распространения гриппа. Согласно полученным результатам, снижение уровня заболеваемости в первом сезоне приведёт к увеличению заболеваемости во втором сезоне. Компенсировать снижение иммунитета населения может помочь расширение масштабов вакцинации. В зависимости от перекрёстного иммунитета от перенесённой ранее инфекции и трансмиссивности штамма уровень заболеваемости может вырасти до 50%.
Многие из рассматриваемых в этом разделе публикаций описывают усложнённые модели, где к базовой версии ИП были добавлены дополнительные параметры. В частности, A. Truszkowska и соавт. модифицировали базовую версию модели добавлением в ИП разделения работоспособного населения на сферы деятельности [44]. Это позволило отразить в модели сложную структуру занятости. А в статье C. Fosco и соавт. рабочая сила была разделена на 4 группы в соответствии с различной мобильностью в случае введения карантинных мер [45].
В ряде работ было уделено большее внимание разделению дня на временные участки. В 24 моделях были учтены временные характеристики мобильности агентов (учёт расписания, деление дня).
К целям подходов, учитывающих и свойства агентов, и свойства локаций, относятся:
- анализ управленческих решений;
- поиск оптимального подхода к осуществлению нефармацевтических вмешательств;
- изучение распространения инфекции с использованием GPS;
- изучение распространения патогена на ранних стадиях;
- изучение распространения разных штаммов;
- моделирование отслеживания контактов и передачи вируса;
- изучение распространения вируса в разных странах/городах;
- изучение стратегий вакцинации;
- изучение защиты населения в зависимости от прошедшего сезона.
При формировании ИП данного типа разработчики моделей часто прибегают к различным упрощениям для возможности включения дополнительных характеристик, имеющих, по их мнению, решающее значение [46]. Некоторые предположения превосходят нынешнее понимание механизмов развития эпидемии, что позволяет включать их в исследование только в приближенной форме [47]. В качестве основы для создания ИП-цифрового двойника принято использовать обновляющиеся реальные данные, которые затем проецируются на выборку меньшего размера, чем население в целом. Даже если выборка повторяет структуру реальной популяции, полученные для неё результаты могут не в полной мере отражать ситуацию в реальной популяции [48].
Усложнение формирования ИП
При создании реалистичной популяции для эпидемиологических исследований необходим обширный набор параметров, учёт каждого из которых на данный момент невозможен. Базовые версии моделей позволяют описывать эпидемиологический процесс в общем виде и проводить исследование закономерностей и поиск тенденций в динамике эпидемий.
В целях большей правдоподобности некоторые авторы прибегали к усложнению ИП путём введения следующих параметров:
- сезонность;
- сопутствующие заболевания;
- динамический иммунитет;
- этническая принадлежность;
- доход;
- транспортные потоки.
Неоднородность популяции с точки зрения восприимчивости индивидов к вирусу и тяжести протекания болезни может быть учтена с помощью фактора сопутствующих заболеваний. В самом простом варианте учёт сопутствующих заболеваний возможен благодаря бинарному параметру (есть или нет) [28]. В более сложном варианте за счёт введения дополнительного модуля расчёта фактора рисков возможен учёт как конкретных заболеваний (диабет 1-го и 2-го типов, гипертония, сердечно-сосудистые заболевания и др.), так и факторов риска, связанных с образом жизни (курение, физическая активность, повышенный индекс массы тела и др.) [49].
В некоторых работах было выполнено моделирование динамического иммунитета. Популярной основой для учёта иммунитета стала модель Covasim [50–52], которая предоставляет возможность динамического изменения значений уровня специфической иммунной защиты для каждого агента и популяции в целом.
Сезонность может влиять как на свойства возбудителя заболевания (в основном используется при моделировании сезонного гриппа), так и на другие параметры (влияние среднесуточной температуры на восприимчивость, влияние времени года на сеть контактов с распределением по полу и др.) [43, 53–58].
При наличии соответствующих данных возможно добавление социологических параметров агентов — уровня дохода и этнической принадлежности, при этом в модели эти характеристики могут отражаться по-разному. В статье M.D. Patel и соавт. люди разной национальности обладали разной восприимчивостью к вирусу и по-разному переносили заболевание [59]. В работе C. Fosco и соавт. уровень дохода влиял на возможность работников оставаться дома во время эпидемии [45]. В статье M. Thakur и соавт. доход прямо коррелировал со снижением уровня вакцинации [60].
Моделирование транспортных потоков внутри ИП было использовано в 15 (10%) работах, 8 из которых учитывали географические и демографические данные о населении, 7 — только демографические.
Представление транспорта было возможно в виде:
- дополнительной случайной сети контактов;
- добавления ячеек транспорта/остановок;
- построения общих маршрутов агентов.
Некоторые исследователи прибегали к разделению транспорта на виды:
- автомобиль, попутный транспорт, общественный транспорт, ходьба и др. (с возможностью заразиться только в автомобиле и общественном транспорте) [25];
- метро, автобус, маршрутное такси [61].
Заключение
Формирование ИП — ключевой момент в построении предсказательных агентных моделей. Использование АОМ позволяет рассматривать популяцию на уровне индивидуальных представителей, что открывает новые возможности для изучения развития эпидемий и анализа мер по предотвращению распространения инфекции.
В нашем обзоре на основании анализа материала 144 оригинальных исследований рассмотрены 4 варианта построения ИП, обладающих разными степенями детализации. Мы намеренно использовали для поиска литературы исключительно базу данных PubMed, поскольку она ориентирована на биомедицинские исследования, включая эпидемиологию. Этот выбор позволил проанализировать основные публикации, опубликованные в рейтинговых рецензируемых журналах в интересующей нас области, но не исключено, что какая-то часть доступных публикаций не была рассмотрена. Также в обзоре были рассмотрены статьи, опубликованные с начала пандемии COVID-19. Это позволило проанализировать наиболее актуальный срез работ, сделав акцент на востребованных решениях в формировании ИП, при этом в обзор не вошли ранее опубликованные модели EpiSimS [62] и TRANSIMS [63].
Надо отметить, что все рассмотренные варианты построения ИП оказались пригодными для решения заявленного разработчиками перечня задач в области эпидемиологии инфекционных заболеваний. Ограничения настоящего исследования продиктованы невозможностью проведения экспериментального подтверждения успешности реализации представленных АОМ для достижения поставленных целей и выполнения задач в рассмотренных исследованиях. В большинстве случаев нет возможности критически осмыслить модель ввиду наличия общего, часто поверхностного описания её устройства, приводимого в публикации, и отсутствия доступа к исходному коду модели. Анализ выбранной литературы проводился в значительной степени на основе оценки результатов авторами работ. В большинстве случаев авторы не приводят анализ чувствительности результата к параметрам моделируемого патогена и ИП. Такой анализ является важной характеристикой сложных моделей и может показать реальную важность параметров, и данный обзор выявил систематический недостаток значительной части проанализированных работ.
Среди выявленных ограничений в создании ИП наиболее существенными являются недостаточность и анахронизм реальных демографических и статистических данных, необходимых для последующего учёта в модели. Работы, учитывающие свойства агентов в ИП, как правило, полагаются на данные переписи населения или социологические опросы, которые не всегда обладают требуемой детализацией. Модели, включающие передвижение агентов на городской карте, используют информацию, полученную из специализированных приложений, баз данных и картографических сервисов, таких как Google Maps и OpenStreetMap. Получение этих данных и их учёт в модели может быть сложной задачей, поэтому в ряде случаев использовали упрощённые модели, основанные на предположениях о поведении и взаимодействии агентов.
Использование сложных и разнообразных реальных демографических и статистических данных возможно при изучении небольших групп (на уровне помещения, здания), однако для более масштабных исследований вычислительная сложность в случае увеличения числа параметров или размера популяции может превысить технические возможности вычисления, привести к получению недостоверных или неинтерпретируемых результатов.
Дальнейшие исследования в области создания и использования ИП при агентном моделировании могут быть направлены на оптимизацию методов параметризации моделей и поиск баланса между детализацией и интерпретируемостью модели для достижения максимальной точности и достоверности результатов. При создании ИП важно учесть факторы, на которые может быть направлен контроль. Это позволит улучшить качество принимаемых решений в области общественного здравоохранения и повысить эффективность противодействия эпидемиям.
Об авторах
Ирина Ильинична Маслова
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0009-0000-0849-9123
студент
Россия, МоскваАлександр Иванович Манолов
Научно-исследовательский институт системной биологии и медицины
Автор, ответственный за переписку.
Email: paraslonic@gmail.com
ORCID iD: 0000-0003-3912-429X
к.б.н., н.с.
Россия, МоскваОксана Евгеньевна Глущенко
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0000-0002-2028-3066
м.н.с.
Россия, МоскваИван Евгеньевич Козлов
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0009-0007-2437-5527
лаборант-исследователь
Россия, МоскваВера Ильинична Цуркис
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0009-0001-5140-0990
студент
Россия, МоскваНиколай Сергеевич Попов
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0009-0002-6450-8594
студент
Россия, МоскваАндрей Евгеньевич Самойлов
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0000-0001-8284-3164
н.с.
Россия, МоскваАлександр Николаевич Лукашев
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0000-0001-7365-0352
д.б.н., член-корр. РАН, г.н.с.
Россия, МоскваЕлена Николаевна Ильина
Научно-исследовательский институт системной биологии и медицины
Email: paraslonic@gmail.com
ORCID iD: 0000-0003-0130-5079
д.б.н., член-корр. РАН, г.н.с., зав. лаб. математической биологии и биоинформатики
Россия, МоскваСписок литературы
- Kirkeby C., Brookes V.J., Ward M.P., et al. A practical introduction to mechanistic modeling of disease transmission in veterinary science. Front. Vet. Sci. 2021;7:546651. DOI: https://doi.org/10.3389/fvets.2020.546651
- Hudson E.G., Brookes V.J., Ward M.P. Demographic studies of owned dogs in the Northern Peninsula Area, Australia, to inform population and disease management strategies. Aust. Vet. J. 2018;96(12):487–94. DOI: https://doi.org/10.1111/avj.12766
- Glushchenko O.E., Prianichnikov N.A., Olekhnovich E.I., et al. VERA: agent-based modeling transmission of antibiotic resistance between human pathogens and gut microbiota. Bioinformatics. 2019;35(19):3803–11. DOI: https://doi.org/10.1093/bioinformatics/btz154
- Decelle A., Krzakala F., Moore C., Zdeborová L. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications. Phys. Rev. E. Stat. Nonlin. Soft Matter. Phys. 2011;84(6 Pt 2):066106. DOI: https://doi.org/10.1103/PhysRevE.84.066106
- Ackland G.J., Ackland J.A., Antonioletti M., Wallace D.J. Fitting the reproduction number from UK coronavirus case data and why it is close to 1. Philos. Trans. A. Math. Phys. Eng. Sci. 2022;380(2233):20210301. DOI: https://doi.org/10.1098/rsta.2021.0301
- Creswell R., Augustin D., Bouros I., et al. Heterogeneity in the onwards transmission risk between local and imported cases affects practical estimates of the time-dependent reproduction number. Philos. Trans. A. Math. Phys. Eng. Sci. 2022;380(2233):20210308. DOI: https://doi.org/10.1098/rsta.2021.0308
- Van Dyke Parunak H., Savit R., Riolo R.L. Agent-based modeling vs. equation-based modeling: A case study and users’ guide. Multi-Agent Systems and Agent-Based Simulation. 2010;1534:10–25. DOI: https://doi.org/10.1007/10692956_2
- Rahmandad H., Sterman J. Heterogeneity and network structure in the dynamics of diffusion: comparing agent-based and differential equation models. Management Science. 2008;54:998–1014. DOI: https://doi.org/10.1287/mnsc.1070.0787
- Shanta S.S., Biswas M.H.A. The impact of media awareness in controlling the spread of infectious diseases in terms of SIR model. Mathematical Modelling of Engineering Problems. 2020;7:368–76. DOI: https://doi.org/10.18280/mmep.070306
- Kerr C.C., Stuart R.M., Mistry D., et al. Covasim: аn agent-based model of COVID-19 dynamics and interventions. PLoS Comput. Biol. 2021;17(7):e1009149. DOI: https://doi.org/10.1371/journal.pcbi.1009149
- Gozzi N., Tizzoni M., Chinazzi M., et al. Estimating the effect of social inequalities on the mitigation of COVID-19 across communities in Santiago de Chile. Nat. Commun. 2021;12(1):2429. DOI: https://doi.org/10.1038/s41467-021-22601-6
- Squazzoni F., Polhill J.G., Edmonds B., et al. Computational models that matter during a global pandemic outbreak: a call to action. Journal of Artificial Societies and Social Simulation. 2020; 23(2). DOI: https://doi.org/10.18564/jasss.4298
- Lux T. The social dynamics of COVID-19. Physica A. 2021;567: 125710. DOI: https://doi.org/10.1016/j.physa.2020.125710
- Conte R., Paolucci M. On agent-based modeling and computational social science. Front. Psychol. 2014;5:668. DOI: https://doi.org/10.3389/fpsyg.2014.00668
- Lux T., Zwinkels R.C. Empirical Validation of Agent-Based Models. In: Handbook of Computational Economics. Volume 4. Elsevier;2018:437–88. DOI: https://doi.org/10.1016/bs.hescom.2018.02.003
- Tracy M., Cerdá M., Keyes K.M. Agent-based modeling in public health: current applications and future directions. Annu. Rev. Public Health. 2018;39:77–94. DOI: https://doi.org/10.1146/annurev-publhealth-040617-014317
- Bonabeau E. Agent-based modeling: methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. U.S.A. 2002;99(Suppl. 3):7280–7. DOI: https://doi.org/10.1073/pnas.082080899
- Marks R.E. Validating simulation models: a general framework and four applied examples. Comput. Econ. 2007;30:265–90. DOI: https://doi.org/10.1007/s10614-007-9101-7
- Whitman J., Jayaprakash C. Stochastic modeling of influenza spread dynamics with recurrences. PLoS One. 2020;15(4): e0231521. DOI: https://doi.org/10.1371/journal.pone.0231521
- Guo X., Tong J., Chen P., Fan W. The suppression effect of emotional contagion in the COVID-19 pandemic: a multi-layer hybrid modelling and simulation approach. PLoS One. 2021;16(7):e0253579. DOI: https://doi.org/10.1371/journal.pone.0253579
- Chung N.N., Chew L.Y. Modelling Singapore COVID-19 pandemic with a SEIR multiplex network model. Sci. Rep. 2021;11(1):10122. DOI: https://doi.org/10.1038/s41598-021-89515-7
- Moghadas S.M., Fitzpatrick M.C., Shoukat A., et al. Simulated identification of silent COVID-19 infections among children and estimated future infection rates with vaccination. JAMA Netw Open. 2021;4(4):e217097. DOI: https://doi.org/10.1001/jamanetworkopen.2021.7097
- Sah P., Vilches T.N., Pandey A., et al. Estimating the impact of vaccination on reducing COVID-19 burden in the United States: December 2020 to March 2022. J. Glob. Health. 2022;12:03062. DOI: https://doi.org/10.7189/jogh.12.03062
- Català M., Li X., Prats C., Prieto-Alhambra D. The impact of prioritisation and dosing intervals on the effects of COVID-19 vaccination in Europe: an agent-based cohort model. Sci. Rep. 2021;11(1):18812. DOI: https://doi.org/10.1038/s41598-021-98216-0
- Truszkowska A., Thakore M., Zino L., et al. Designing the safe reopening of US towns through high-resolution agent-based modeling. Adv. Theory Simul. 2021;4(9):2100157. DOI: https://doi.org/10.1002/adts.202100157
- Truszkowska A., Zino L., Butail S., et al. Exploring a COVID-19 Endemic scenario: high-resolution agent-based modeling of multiple variants. Adv. Theory Simul. 2023;6(1):2200481. DOI: https://doi.org/10.1002/adts.202200481
- Truszkowska A., Zino L., Butail S., et al. Predicting the effects of waning vaccine immunity against COVID-19 through high-resolution agent-based modeling. Adv. Theory Simul. 2022;5(6):2100521. DOI: https://doi.org/10.1002/adts.202100521
- Hadley E., Rhea S., Jones K., et al. Enhancing the prediction of hospitalization from a COVID-19 agent-based model: A Bayesian method for model parameter estimation. PLoS One. 2022;17(3):e0264704. DOI: https://doi.org/10.1371/journal.pone.0264704
- Rodríguez J.P., Aleta A., Moreno Y. Digital cities and the spread of COVID-19: Characterizing the impact of non-pharmaceutical interventions in five cities in Spain. Front. Public Health. 2023;11:1122230. DOI: https://doi.org/10.3389/fpubh.2023.1122230
- Chiba A. Modeling the effects of contact-tracing apps on the spread of the coronavirus disease: Mechanisms, conditions, and efficiency. PLoS One. 2021;16(9):e0256151. DOI: https://doi.org/10.1371/journal.pone.0256151
- Cattaneo A., Vitali A., Mazzoleni M., Previdi F. An agent-based model to assess large-scale COVID-19 vaccination campaigns for the Italian territory: The case study of Lombardy region. Comput. Methods Programs Biomed. 2022;224:107029. DOI: https://doi.org/10.1016/j.cmpb.2022.107029
- Krivorotko O., Sosnovskaia M., Vashchenko I., et al. Agent-based modeling of COVID-19 outbreaks for New York state and UK: Parameter identification algorithm. Infect. Dis. Model. 2022;7(1):30–44. DOI: https://doi.org/10.1016/j.idm.2021.11.004
- Koichubekov B., Takuadina A., Korshukov I., et al. The epidemiological and economic impact of COVID-19 in Kazakhstan: An agent-based modeling. Healthcare (Basel). 2023;11(22):2968. DOI: https://doi.org/10.3390/healthcare11222968
- Hinch R., Probert W.J.M., Nurtay A., et al. OpenABM-COVID19 – an agent-based model for non-pharmaceutical interventions against COVID-19 including contact tracing. PLoS Comput. Biol. 2021;17(7):e1009146. DOI: https://doi.org/10.1371/journal.pcbi.1009146
- Daghriri T., Ozmen O. Quantifying the effects of social distancing on the spread of COVID-19. Int. J. Environ. Res. Public Health. 2021;18(11):5566. DOI: https://doi.org/10.3390/ijerph18115566
- Li H., Zhang H. Cost-effectiveness analysis of COVID-19 screening strategy under China's dynamic zero-case policy. Front. Public Health. 2023;11:1099116. DOI: https://doi.org/10.3389/fpubh.2023.1099116
- Wang Q., Shi N., Huang J., et al. Cost-effectiveness of public health measures to control COVID-19 in China: A microsimulation modeling study. Front. Public Health. 2022;9:726690. DOI: https://doi.org/10.3389/fpubh.2021.726690
- Kishore N., Kahn R., Martinez P.P., et al. Lockdowns result in changes in human mobility which may impact the epidemiologic dynamics of SARS-CоV-2. Sci. Rep. 2021;11(1):6995. DOI: https://doi.org/10.1038/s41598-021-86297-w
- Grefenstette J.J., Brown S.T., Rosenfeld R., et al. FRED (a Framework for Reconstructing Epidemic Dynamics): an open-source software system for modeling infectious diseases and control strategies using census-based populations. BMC Public Health. 2013;13:940. DOI: https://doi.org/10.1186/1471-2458-13-940
- Krauland M.G., Zimmerman R.K., Williams K.V., et al. Agent-based model of the impact of higher influenza vaccine efficacy on seasonal influenza burden. Vaccine X. 2023;13:100249. DOI: https://doi.org/10.1016/j.jvacx.2022.100249
- Williams K.V., Krauland M.G., Harrison L.H., et al. Can a two-dose influenza vaccine regimen better protect older adults? An agent-based modeling study. Vaccines (Basel). 2022;10(11):1799. DOI: https://doi.org/10.3390/vaccines10111799
- Woodul R.L., Delamater P.L., Woodburn M. Validating model output in the absence of ground truth data: a COVID-19 case study using the Simulator of Infectious Disease Dynamics in North Carolina (SIDD-NC) model. Health Place. 2023;83:103065. DOI: https://doi.org/10.1016/j.healthplace.2023.103065
- Krauland M.G., Galloway D.D., Raviotta J.M., et al. Impact of low rates of influenza on next-season influenza infections. Am. J. Prev. Med. 2022;62(4):503–10. DOI: https://doi.org/10.1016/j.amepre.2021.11.007
- Truszkowska A., Fayed M., Wei S., et al. Urban determinants of COVID-19 spread: a comparative study across three cities in New York state. J. Urban. Health. 2022;99(5):909–21. DOI: https://doi.org/10.1007/s11524-022-00623-9
- Fosco C., Zurita F. Assessing the short-run effects of lockdown policies on economic activity, with an application to the Santiago Metropolitan Region, Chile. PLoS One. 2021;16(6):e0252938. DOI: https://doi.org/10.1371/journal.pone.0252938
- Maziarz M., Zach M. Agent-based modelling for SARS-CоV-2 epidemic prediction and intervention assessment: A methodological appraisal. J. Eval. Clin. Pract. 2020; 26(5): 1352–60. DOI: https://doi.org/10.1111/jep.13459
- Gupta P., Maharaj T., Weiss M., et al. Proactive contact tracing. PLOS Digit. Health. 2023;2(3):e0000199. DOI: https://doi.org/10.1371/journal.pdig.0000199
- Staffini A., Svensson A.K., Chung U.I., Svensson T. An agent-based model of the local spread of SARS-CоV-2: modeling study. JMIR Med. Inform. 2021;9(4):e24192. DOI: https://doi.org/10.2196/24192
- Mintram K., Anagnostou A., Anokye N., et al. CALMS: Modelling the long-term health and economic impact of COVID-19 using agent-based simulation. PLoS One. 2022;17(8):e0272664. DOI: https://doi.org/10.1371/journal.pone.0272664
- Silva M.E.P., Fyles M., Pi L., et al. The role of regular asymptomatic testing in reducing the impact of a COVID-19 wave. Epidemics. 2023;44:100699. DOI: https://doi.org/10.1016/j.epidem.2023.100699
- Pham Q.D., Stuart R.M., Nguyen T.V., et al. Estimating and mitigating the risk of COVID-19 epidemic rebound associated with reopening of international borders in Vietnam: a modelling study. Lancet Glob. Health. 2021;9(7):e916–24. DOI: https://doi.org/10.1016/s2214-109x(21)00103-0
- Sanz-Leon P., Hamilton L.H.W., Raison S.J., et al. Modelling herd immunity requirements in Queensland: impact of vaccination effectiveness, hesitancy and variants of SARS-CоV-2. Philos. Trans. A. Math. Phys. Eng. Sci. 2022;380(2233):20210311. DOI: https://doi.org/10.1098/rsta.2021.0311
- Pais C.M., Godano M.I., Juarez E., et al. City-scale model for COVID-19 epidemiology with mobility and social activities represented by a set of hidden Markov models. Comput. Biol. Med. 2023;160:106942. DOI: https://doi.org/10.1016/j.compbiomed.2023.106942
- Reguly I.Z., Csercsik D., Juhász J., et al. Microsimulation based quantitative analysis of COVID-19 management strategies. PLoS Comput. Biol. 2022;18(1):e1009693. DOI: https://doi.org/10.1371/journal.pcbi.1009693
- Barthe G., Viti R., Druschel P., et al. Listening to Bluetooth beacons for epidemic risk mitigation. Sci. Rep. 2022;12(1):5558. DOI: https://doi.org/10.1038/s41598-022-09440-1
- Bicher M., Rippinger C., Schneckenreither G., et al. Model based estimation of the SARS-CоV-2 immunization level in austria and consequences for herd immunity effects. Sci. Rep. 2022;12(1):2872. DOI: https://doi.org/10.1038/s41598-022-06771-x
- Nagpal S., Kumar R., Noronha R.F., et al. Seasonal variations in social contact patterns in a rural population in north India: Implications for pandemic control. PLoS One. 2024;19(2):e0296483. DOI: https://doi.org/10.1371/journal.pone.0296483
- Souther A., Chang M.H., Tassier T. It's worth a shot: urban density, endogenous vaccination decisions, and dynamics of infectious disease. J. Econ. Interact. Coord. 2023;18(1):163–89. DOI: https://doi.org/10.1007/s11403-022-00367-4
- Patel M.D., Rosenstrom E., Ivy J.S., et al. Association of simulated COVID-19 vaccination and nonpharmaceutical interventions with infections, hospitalizations, and mortality. JAMA Netw. Open. 2021;4(6):e2110782. DOI: https://doi.org/10.1001/jamanetworkopen.2021.10782
- Thakur M., Zhou R., Mohan M., et al. COVID's collateral damage: likelihood of measles resurgence in the United States. BMC Infect. Dis. 2022;22(1):743. DOI: https://doi.org/10.1186/s12879-022-07703-w
- Rykovanov G.N., Lebedev S.N., Zatsepin O.V., et al. Agent-based simulation of the COVID-19 epidemic in Russia. Her. Russ. Acad. Sci. 2022;92(4):479–87. DOI: https://doi.org/10.1134/s1019331622040219
- Stroud P., Del Valle S., Sydoriak S., et al. Spatial dynamics of pandemic influenza in a massive artificial society, journal of artificial societies and social simulation. J. Artif. Soc. Soc. Simul. 2007; 10(4): 1–9.
- Barrett C.L., Beckman R.J., Berkbigler K.P., et al. TRANSIMS: Transportation analysis simulation system. In: Portland Study Reports. Los Alamos, NM;1999.
- Kaxiras E., Neofotistos G. Multiple epidemic wave model of the COVID-19 pandemic: modeling study. J. Med. Internet Res. 2020;22(7):e20912. DOI: https://doi.org/10.2196/20912
- Quilty B.J., Clifford S., Hellewell J., et al. Quarantine and testing strategies in contact tracing for SARS-CоV-2: a modelling study. Lancet Public Health. 2021;6(3):e175–83. DOI: https://doi.org/10.1016/s2468-2667(20)30308-x
- Gwizdałła T. Viral disease spreading in grouped population. Comput. Methods Programs Biomed. 2020;197:105715. DOI: https://doi.org/10.1016/j.cmpb.2020.105715
- Sood M., Sridhar A., Eletreby R., et al. Spreading processes with mutations over multilayer networks. Proc. Natl. Acad. Sci. U.S.A. 2023;120(24):e2302245120. DOI: https://doi.org/10.1073/pnas.2302245120
- Streilein W., Finklea L., Schuldt D., et al. Evaluating COVID-19 exposure notification effectiveness with SimAEN: A simulation tool designed for public health decision making. Public Health Rep. 2022;137(2_suppl):83S–9S. DOI: https://doi.org/10.1177/00333549221116361
- Kim Y., Ryu H., Lee S. Effectiveness of intervention strategies on MERS-CoV transmission dynamics in South Korea, 2015: Simulations on the network based on the real-world contact data. Int. J. Environ. Res. Public Health. 2021;18(7):3530. DOI: https://doi.org/10.3390/ijerph18073530
- Kwon O., Son W.S., Kim J.Y., Kim J.H. Intervention effects in the transmission of COVID-19 depending on the detection rate and extent of isolation. Epidemiol. Health. 2020;42:e2020045. DOI: https://doi.org/10.4178/epih.e2020045
- Tatsukawa Y., Arefin M.R., Kuga K., Tanimoto J. An agent-based nested model integrating within-host and between-host mechanisms to predict an epidemic. PLoS One. 2023;18(12):e0295954. DOI: https://doi.org/10.1371/journal.pone.0295954
- Stapelberg N.J.C., Smoll N.R., Randall M., et al. A Discrete-Event, Simulated Social Agent-Based Network Transmission (DESSABNeT) model for communicable diseases: Method and validation using SARS-CоV-2 data in three large Australian cities. PLoS One. 2021;16(5):e0251737. DOI: https://doi.org/10.1371/journal.pone.0251737
- Thompson J., McClure R., Blakely T., et al. Modelling SARS-CоV-2 disease progression in Australia and New Zealand: an account of an agent-based approach to support public health decision-making. Aust. N. Z. J. Public Health. 2022;46(3):292–303. DOI: https://doi.org/10.1111/1753-6405.13221
- Hinch R., Panovska-Griffiths J., Probert W.J.M., et al. Estimating SARS-CоV-2 variant fitness and the impact of interventions in England using statistical and geo-spatial agent-based models. Philos. Trans. A. Math. Phys. Eng. Sci. 2022;380(2233):20210304. DOI: https://doi.org/10.1098/rsta.2021.0304
- Tatapudi H., Das R., Das T.K. Impact assessment of full and partial stay-at-home orders, face mask usage, and contact tracing: An agent-based simulation study of COVID-19 for an urban region. Glob. Epidemiol. 2020;2:100036. DOI: https://doi.org/10.1016/j.gloepi.2020.100036
- Jahn B., Sroczynski G., Bicher M., et al. Targeted COVID-19 vaccination (TAV-COVID) considering limited vaccination capacities – an agent-based modeling evaluation. Vaccines (Basel). 2021;9(5):434. DOI: https://doi.org/10.3390/vaccines9050434
- Tatapudi H., Das T.K. Impact of school reopening on pandemic spread: a case study using an agent-based model for COVID-19. Infect. Dis. Model. 2021;6:839–47. DOI: https://doi.org/10.1016/j.idm.2021.06.007
- Romero-Brufau S., Chopra A., Ryu A.J., et al. Public health impact of delaying second dose of BNT162b2 or mRNA-1273 covid-19 vaccine: simulation agent based modeling study. BMJ. 2021;373:n1087. DOI: https://doi.org/10.1136/bmj.n1087
- Goldenbogen B., Adler S.O., Bodeit O., et al. Control of COVID-19 outbreaks under stochastic community dynamics, bimodality, or limited vaccination. Adv. Sci. (Weinh). 2022;9(23):e2200088. DOI: https://doi.org/10.1002/advs.202200088
- Moghadas S.M., Vilches T.N., Zhang K., et al. Evaluation of COVID-19 vaccination strategies with a delayed second dose. PLoS Biol. 2021;19(4):e3001211. DOI: https://doi.org/10.1371/journal.pbio.3001211
- Keskinocak P., Oruc B.E., Baxter A., et al. The impact of social distancing on COVID19 spread: State of Georgia case study. PLoS One. 2020;15(10):e0239798. DOI: https://doi.org/10.1371/journal.pone.0239798
- Berec L., Diviák T., Kuběna A., et al. On the contact tracing for COVID-19: A simulation study. Epidemics. 2023;43:100677. DOI: https://doi.org/10.1016/j.epidem.2023.100677
- Moghadas S.M., Fitzpatrick M.C., Sah P., et al. The implications of silent transmission for the control of COVID-19 outbreaks. Proc. Natl. Acad. Sci. U.S.A. 2020;117(30):17513–5. DOI: https://doi.org/10.1073/pnas.2008373117
- Ben-Zuk N., Daon Y., Sasson A., et al. Assessing COVID-19 vaccination strategies in varied demographics using an individual-based model. Front. Public Health. 2022;10:966756. DOI: https://doi.org/10.3389/fpubh.2022.966756
- Nguyen Q.D., Prokopenko M. A general framework for optimising cost-effectiveness of pandemic response under partial intervention measures. Sci. Rep. 2022;12(1):19482. DOI: https://doi.org/10.1038/s41598-022-23668-x
- Abdollahi E., Haworth-Brockman M., Keynan Y., et al. Simulating the effect of school closure during COVID-19 outbreaks in Ontario, Canada. BMC Med. 2020;18(1):230. DOI: https://doi.org/10.1186/s12916-020-01705-8
- Zhang K., Vilches T.N., Tariq M., et al. The impact of mask-wearing and shelter-in-place on COVID-19 outbreaks in the United States. Int. J. Infect. Dis. 2020;101:334–41. DOI: https://doi.org/10.1016/j.ijid.2020.10.002
- Shoukat A., Wells C.R., Langley J.M., et al. Projecting demand for critical care beds during COVID-19 outbreaks in Canada. CMAJ. 2020;192(19):E489–96. DOI: https://doi.org/10.1503/cmaj.200457
- Eilersen A., Sneppen K. Cost-benefit of limited isolation and testing in COVID-19 mitigation. Sci. Rep. 2020;10(1):18543. DOI: https://doi.org/10.1038/s41598-020-75640-2
- Hotton A.L., Ozik J., Kaligotla C., et al. Impact of changes in protective behaviors and out-of-household activities by age on COVID-19 transmission and hospitalization in Chicago, Illinois. Ann. Epidemiol. 2022;76:165–73. DOI: https://doi.org/10.1016/j.annepidem.2022.06.005
- Aleta A., Martín-Corral D., Bakker M.A., et al. Quantifying the importance and location of SARS-CоV-2 transmission events in large metropolitan areas. Proc. Natl. Acad. Sci. U.S.A. 2022;119(26):e2112182119. DOI: https://doi.org/10.1073/pnas.2112182119
- Bicher M., Rippinger C., Zechmeister M., et al. An iterative algorithm for optimizing COVID-19 vaccination strategies considering unknown supply. PLoS One. 2022;17(5):e0265957. DOI: https://doi.org/10.1371/journal.pone.0265957
- Nishi A., Dewey G., Endo A., et al. Network interventions for managing the COVID-19 pandemic and sustaining economy. Proc. Natl. Acad. Sci. U.S.A. 2020;117(48):30285–94. DOI: https://doi.org/10.1073/pnas.2014297117
- Weng X., Chen Q., Sathapathi T.K., et al. Impact of school operating scenarios on COVID-19 transmission under vaccination in the U.S.: an agent-based simulation model. Sci. Rep. 2023;13(1):12836. DOI: https://doi.org/10.1038/s41598-023-37980-7
- Vilches T.N., Abdollahi E., Cipriano L.E., et al. Impact of non-pharmaceutical interventions and vaccination on COVID-19 outbreaks in Nunavut, Canada: a Canadian Immunization Research Network (CIRN) study. BMC Public Health. 2022;22(1):1042. DOI: https://doi.org/10.1186/s12889-022-13432-1
- Ng V., Fazil A., Waddell L.A., et al. Projected effects of nonpharmaceutical public health interventions to prevent resurgence of SARS-CоV-2 transmission in Canada. CMAJ. 2020;192(37):E1053–64. DOI: https://doi.org/10.1503/cmaj.200990
- Scott N., Abeysuriya R.G., Delport D., et al. COVID-19 epidemic modelling for policy decision support in Victoria, Australia 2020-2021. BMC Public Health. 2023;23(1):988. DOI: https://doi.org/10.1186/s12889-023-15936-w
- Moghadas S.M., Vilches T.N., Zhang K., et al. The impact of vaccination on coronavirus disease 2019 (COVID-19) outbreaks in the United States. Clin. Infect. Dis. 2021;73(12):2257–64. DOI: https://doi.org/10.1093/cid/ciab079
- Alagoz O., Sethi A.K., Patterson B.W., et al. Effect of timing of and adherence to social distancing measures on COVID-19 burden in the United States: A simulation modeling approach. Ann. Intern. Med. 2021;174(1):50–7. DOI: https://doi.org/10.7326/m20-4096
- Shi P., Yan J., Keskinocak P., et al. The impact of opening dedicated clinics on disease transmission during an influenza pandemic. PLoS One. 2020;15(8):e0236455. DOI: https://doi.org/10.1371/journal.pone.0236455
- Wu S., Huang Z., Grant-Muller S., et al. Modelling the reopen strategy from dynamic zero-COVID in China considering the sequela and reinfection. Sci. Rep. 2023;13(1):7343. DOI: https://doi.org/10.1038/s41598-023-34207-7
- Moreno López J.A., Arregui García B., Bentkowski P., et al. Anatomy of digital contact tracing: Role of age, transmission setting, adoption, and case detection. Sci. Adv. 2021;7(15):eabd8750. DOI: https://doi.org/10.1126/sciadv.abd8750
- Scott N., Palmer A., Delport D., et al. Modelling the impact of relaxing COVID-19 control measures during a period of low viral transmission. Med. J. Aust. 2021;214(2):79–83. DOI: https://doi.org/10.5694/mja2.50845
- Abeysuriya R.G., Delport D., Stuart R.M., et al. Preventing a cluster from becoming a new wave in settings with zero community COVID-19 cases. BMC Infect. Dis. 2022;22(1):232. DOI: https://doi.org/10.1186/s12879-022-07180-1
- Houdroge F., Palmer A., Delport D., et al. Frequent and unpredictable changes in COVID-19 policies and restrictions reduce the accuracy of model forecasts. Sci. Rep. 2023;13(1):1398. DOI: https://doi.org/10.1038/s41598-023-27711-3
- Sneppen K., Nielsen B.F., Taylor R.J., Simonsen L. Overdispersion in COVID-19 increases the effectiveness of limiting nonrepetitive contacts for transmission control. Proc. Natl. Acad. Sci. U.S.A. 2021;118(14):e2016623118. DOI: https://doi.org/10.1073/pnas.2016623118
- Zhang X., Chen B., Le J., Hu Y. Impact of different nucleic acid testing scenarios on COVID-19 transmission. Heliyon. 2023;10(1):e23700. DOI: https://doi.org/10.1016/j.heliyon.2023.e23700
- Li A., Wu J., Moghadas S.M. Epidemic dynamics with time-varying transmission risk reveal the role of disease stage-dependent infectiousness. J. Theor. Biol. 2023;573:111594. DOI: https://doi.org/10.1016/j.jtbi.2023.111594
- Delport D., Sacks-Davis R., Abeysuriya R.G., et al. Lives saved by public health restrictions over the Victorian COVID-19 Delta variant epidemic wave, Aug-Nov 2021. Epidemics. 2023;44:100702. DOI: https://doi.org/10.1016/j.epidem.2023.100702
- Han A.X., Girdwood S.J., Khan S., et al. Strategies for using antigen rapid diagnostic tests to reduce transmission of severe acute respiratory syndrome coronavirus 2 in low- and middle-income countries: a mathematical modelling study applied to Zambia. Clin. Infect. Dis. 2023;76(4):620–30. DOI: https://doi.org/10.1093/cid/ciac814
- Zachreson C., Fair K.M., Harding N., Prokopenko M. Interfering with influenza: nonlinear coupling of reactive and static mitigation strategies. J. R. Soc. Interface. 2020;17(165):20190728. DOI: https://doi.org/10.1098/rsif.2019.0728
- Pandey A., Fitzpatrick M.C., Moghadas S..M, et al. Modelling the impact of a high-uptake bivalent booster scenario on the COVID-19 burden and healthcare costs in New York City. Lancet Reg. Health Am. 2023;24:100555. DOI: https://doi.org/10.1016/j.lana.2023.100555
- Sanz-Leon P., Stevenson N.J., Stuart R.M., et al. Risk of sustained SARS-CоV-2 transmission in Queensland, Australia. Sci. Rep. 2022;12(1):6309. DOI: https://doi.org/10.1038/s41598-022-10349-y
- Groves-Kirkby N., Wakeman E., Patel S., et al. Large-scale calibration and simulation of COVID-19 epidemiologic scenarios to support healthcare planning. Epidemics. 2023;42:100662. DOI: https://doi.org/10.1016/j.epidem.2022.100662
- Sah P., Vilches T.N., Moghadas S.M., et al. Return on investment of the COVID-19 vaccination campaign in New York city. JAMA Netw Open. 2022;5(11):e2243127. DOI: https://doi.org/10.1001/jamanetworkopen.2022.43127
- Goldberg L.A., Jorritsma J., Komjáthy J., Lapinskas J. Increasing efficacy of contact-tracing applications by user referrals and stricter quarantining. PLoS One. 2021;16(5):e0250435. DOI: https://doi.org/10.1371/journal.pone.0250435
- Zhu Y., Shen R., Dong H., Wang W. Spatial heterogeneity and infection patterns on epidemic transmission disclosed by a combined contact-dependent dynamics and compartmental model. PLoS One. 2023;18(6):e0286558. DOI: https://doi.org/10.1371/journal.pone.0286558
- Giacopelli G. A full-scale agent-based model to hypothetically explore the impact of lockdown, social distancing, and vaccination during the COVID-19 pandemic in Lombardy, Italy: model development. JMIRx Med. 2021;2(3):e24630. DOI: https://doi.org/10.2196/24630
- Kustudic M., Niu B., Liu Q. Agent-based analysis of contagion events according to sourcing locations. Sci. Rep. 2021;11(1):16032. DOI: https://doi.org/10.1038/s41598-021-95336-5
- Lima L.L., Atman A.P.F. Impact of mobility restriction in COVID-19 superspreading events using agent-based model. PLoS One. 2021;16(3):e0248708. DOI: https://doi.org/10.1371/journal.pone.0248708
- Eilersen A., Sneppen K. SARS-CоV-2 superspreading in cities vs the countryside. APMIS. 2021;129(7):401–7. DOI: https://doi.org/10.1111/apm.13120
- Gugole F., Coffeng L.E., Edeling W., et al. Uncertainty quantification and sensitivity analysis of COVID-19 exit strategies in an individual-based transmission model. PLoS Comput. Biol. 2021;17(9):e1009355. DOI: https://doi.org/10.1371/journal.pcbi.1009355
- Wallentin G., Kaziyeva D., Reibersdorfer-Adelsberger E. COVID-19 intervention scenarios for a long-term disease management. Int. J. Health Policy Manag. 2020;9(12):508–16. DOI: https://doi.org/10.34172/ijhpm.2020.130
- Bissett K.R., Cadena J., Khan M., Kuhlman C.J. Agent-Based Computational Epidemiological Modeling. J. Indian Inst. Sci. 2021;101(3):303–27. DOI: https://doi.org/10.1007/s41745-021-00260-2
- Murakami T., Sakuragi S., Deguchi H., Nakata M. Agent-based model using GPS analysis for infection spread and inhibition mechanism of SARS-CоV-2 in Tokyo. Sci. Rep. 2022;12(1):20896. DOI: https://doi.org/10.1038/s41598-022-25480-z
- Truszkowska A., Behring B., Hasanyan J., et al. High-resolution agent-based modeling of COVID-19 spreading in a small town. Adv. Theory Simul. 2021;4(3):2000277. DOI: https://doi.org/10.1002/adts.202000277
- Dong T., Dong W., Xu Q. Agent simulation model of COVID-19 epidemic agent-based on GIS: A case study of Huangpu district, Shanghai. Int. J. Environ. Res. Public Health. 2022;19(16):10242. DOI: https://doi.org/10.3390/ijerph191610242
- Castro B.M., Reis M.M., Salles R.M. Multi-agent simulation model updating and forecasting for the evaluation of COVID-19 transmission. Sci. Rep. 2022;12(1):22091. DOI: https://doi.org/10.1038/s41598-022-22945-z
- Gostoli U., Silverman E. An agent-based model of social care provision during the early stages of Covid-19. Sci. Rep. 2022;12(1):16534. DOI: https://doi.org/10.1038/s41598-022-20846-9
- Chang S.L., Cliff O.M., Zachreson C., Prokopenko M. Simulating transmission scenarios of the delta variant of SARS-CоV-2 in Australia. Front. Public Health. 2022;10:823043. DOI: https://doi.org/10.3389/fpubh.2022.823043
- Nguyen Q.D., Chang S.L., Jamerlan C.M., Prokopenko M. Measuring unequal distribution of pandemic severity across census years, variants of concern and interventions. Popul. Health Metr. 2023;21(1):17. DOI: https://doi.org/10.1186/s12963-023-00318-6
- Zhang H., Yin L., Mao L., et al. Combinational recommendation of vaccinations, mask-wearing, and home-quarantine to control influenza in megacities: an agent-based modeling study with large-scale trajectory data. Front. Public Health. 2022;10:883624. DOI: https://doi.org/10.3389/fpubh.2022.883624
- Li Q., Huang Y. Optimizing global COVID-19 vaccine allocation: An agent-based computational model of 148 countries. PLoS Comput. Biol. 2022;18(9):e1010463. DOI: https://doi.org/10.1371/journal.pcbi.1010463
- Kirpich A., Koniukhovskii V., Shvartc V., et al. Development of an interactive, agent-based local stochastic model of COVID-19 transmission and evaluation of mitigation strategies illustrated for the state of Massachusetts, USA. PLoS One. 2021;16(2):e0247182. DOI: https://doi.org/10.1371/journal.pone.0247182
- Singh D.E., Olmedo Luceron C., Limia Sanchez A., et al. Evaluation of vaccination strategies for the metropolitan area of Madrid via agent-based simulation. BMJ Open. 2022;12(12):e065937. DOI: https://doi.org/10.1136/bmjopen-2022-065937
- Alzu'bi A.A., Alasal S.I.A., Watzlaf V.J.M. A Simulation study of coronavirus as an epidemic disease using agent-based modeling. Perspect. Health Inf. Manag. 2020;18(Winter):1g.
- De-Leon H., Aran D. MAM: Flexible Monte-Carlo Agent based model for modelling COVID-19 spread. J. Biomed. Inform. 2023;141:104364. DOI: https://doi.org/10.1016/j.jbi.2023.104364
- Thompson J., Wattam S. Estimating the impact of interventions against COVID-19: From lockdown to vaccination. PLoS One. 2021;16(12):e0261330. DOI: https://doi.org/10.1371/journal.pone.0261330
- Gomez J., Prieto J., Leon E., Rodríguez A. INFEKTA-An agent-based model for transmission of infectious diseases: The COVID-19 case in Bogotá, Colombia. PLoS One. 2021;16(2):e0245787. DOI: https://doi.org/10.1371/journal.pone.0245787
- Schröder M., Bossert A., Kersting M., et al. COVID-19 in South Africa: outbreak despite interventions. Sci. Rep. 2021;11(1):4956. DOI: https://doi.org/10.1038/s41598-021-84487-0.
- Hunter E., Namee B.M., Kelleher J.D. A Model for the spread of infectious diseases in a region. Int. J. Environ. Res. Public Health. 2020;17(9):3119. DOI: https://doi.org/10.3390/ijerph17093119
- Zachreson C., Chang S.L., Cliff O.M., Prokopenko M. How will mass-vaccination change COVID-19 lockdown requirements in Australia? Lancet Reg. Health West Pac. 2021;14:100224. DOI: https://doi.org/10.1016/j.lanwpc.2021.100224
- Guzmán-Merino M., Durán C., Marinescu M.C., et al. Assessing population-sampling strategies for reducing the COVID-19 incidence. Comput. Biol. Med. 2021;139:104938. DOI: https://doi.org/10.1016/j.compbiomed.2021.104938
- Gaudou B., Huynh N.Q., Philippon D., et al. COMOKIT: A modeling kit to understand, analyze, and compare the impacts of mitigation policies against the COVID-19 epidemic at the scale of a city. Front. Public Health. 2020;8:563247. DOI: https://doi.org/10.3389/fpubh.2020.563247
- Chang S.L., Harding N., Zachreson C., et al. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020;11(1):5710. DOI: https://doi.org/10.1038/s41467-020-19393-6
- Harding N., Spinney R., Prokopenko M. Phase transitions in spatial connectivity during influenza pandemics. Entropy (Basel). 2020;22(2):133. DOI: https://doi.org/10.3390/e22020133
- Parisi A., Brand S.P.C., Hilton J., et al. Spatially resolved simulations of the spread of COVID-19 in three European countries. PLoS Comput. Biol. 2021;17(7):e1009090. DOI: https://doi.org/10.1371/journal.pcbi.1009090
- Germann T.C., Smith M.Z., Dauelsberg L.R., et al. Assessing K-12 school reopenings under different COVID-19 spread scenarios — United States, school year 2020/21: а retrospective modeling study. Epidemics. 2022;41:100632. DOI: https://doi.org/10.1016/j.epidem.2022.100632
- Mokhtari A., Mineo C., Kriseman J., et al. A multi-method approach to modeling COVID-19 disease dynamics in the United States. Sci Rep. 2021;11(1):12426. DOI: https://doi.org/10.1038/s41598-021-92000-w
- Gabler J., Raabe T., Röhrl K., Gaudecker H.V. The effectiveness of testing, vaccinations and contact restrictions for containing the CoViD-19 pandemic. Sci. Rep. 2022;12(1):8048. DOI: https://doi.org/10.1038/s41598-022-12015-9
- Milne G.J., Carrivick J., Whyatt D. Mitigating the SARS-CоV-2 Delta disease burden in Australia by non-pharmaceutical interventions and vaccinating children: a modelling analysis. BMC Med. 2022;20(1):80. DOI: https://doi.org/10.1186/s12916-022-02241-3
- Szanyi J., Wilson T., Howe S., et al. Epidemiologic and economic modelling of optimal COVID-19 policy: public health and social measures, masks and vaccines in Victoria, Australia. Lancet Reg. Health West Pac. 2023;32:100675. DOI: https://doi.org/10.1016/j.lanwpc.2022.100675
- Jackson M.L. Low-impact social distancing interventions to mitigate local epidemics of SARS-CоV-2. Microbes Infect. 2020;22(10):611–6. DOI: https://doi.org/10.1016/j.micinf.2020.09.006
- Gankin Y., Nemira A., Koniukhovskii V., et al. Investigating the first stage of the COVID-19 pandemic in Ukraine using epidemiological and genomic data. Infect. Genet. Evol. 2021;95:105087. DOI: https://doi.org/10.1016/j.meegid.2021.105087
- Zhang N., Jack Chan P.T., Jia W., et al. Analysis of efficacy of intervention strategies for COVID-19 transmission: a case study of Hong Kong. Environ. Int. 2021;156:106723. DOI: https://doi.org/10.1016/j.envint.2021.106723
- Nguyen Q.D., Chang S.L., Jamerlan C.M., Prokopenko M. Measuring unequal distribution of pandemic severity across census years, variants of concern and interventions. Popul. Health Metr. 2023;21(1):17. DOI: https://doi.org/10.1186/s12963-023-00318-6
- Aleta A., Martín-Corral D., Pastore Y. Piontti A., et al. Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19. Nat. Hum. Behav. 2020;4(9):964–71. DOI: https://doi.org/10.1038/s41562-020-0931-9
- Zhao C., Zhang J., Hou X., et al. A high-frequency mobility big-data reveals how COVID-19 spread across professions, locations and age groups. PLoS Comput. Biol. 2023;19(4): e1011083. DOI: https://doi.org/10.1371/journal.pcbi.1011083
- Li K.K.F., Jarvis S.A., Minhas F. Elementary effects analysis of factors controlling COVID-19 infections in computational simulation reveals the importance of social distancing and mask usage. Comput. Biol. Med. 2021;134:104369. DOI: https://doi.org/10.1016/j.compbiomed.2021.104369
- Lei H., Zhang N., Niu B., et al. Effect of rapid urbanization in mainland China on the seasonal influenza epidemic: spatiotemporal analysis of surveillance data from 2010 to 2017. JMIR Public Health Surveill. 2023;9:e41435. DOI: https://doi.org/10.2196/41435
- Chiba A. The effectiveness of mobility control, shortening of restaurants' opening hours, and working from home on control of COVID-19 spread in Japan. Health Place. 2021;70:102622. DOI: https://doi.org/10.1016/j.healthplace.2021.102622
- Wang Y., Sun K., Pan Y., et al. A Retrospective modeling study of the targeted non-pharmaceutical interventions during the Xinfadi outbreak in the early stage of the COVID-19 pandemic — Beijing, China, 2020. China CDC Wkly. 2023;5(5):108–12. DOI: https://doi.org/10.46234/ccdcw2023.020
- Latkowski R., Dunin-Kȩplicz B. An agent-based COVID-19 simulator: extending Covasim to the polish context. Procedia Comput. Sci. 2021;192:3607–16. DOI: https://doi.org/10.1016/j.procs.2021.09.134
- Koo J.R., Cook A.R., Park M., et al. Interventions to mitigate early spread of SARS-CоV-2 in Singapore: a modelling study. Lancet Infect. Dis. 2020;20(6):678–88. DOI: https://doi.org/10.1016/s1473-3099(20)30162-6
- Rippinger C., Bicher M., Urach C., et al. Evaluation of undetected cases during the COVID-19 epidemic in Austria. BMC Infect. Dis. 2021;21(1):70. DOI: https://doi.org/10.1186/s12879-020-05737-6
Дополнительные файлы